(Les informations de cet article datent d’octobre 2020)

Ravie de vous retrouver.

Cette photo fut à l’époque beaucoup médiatisée. En avril 2017, pour la 1re fois, un train de marchandises relie Londres à Yiwu, en Chine. Un voyage de 12 000 km en 3 semaines et le message de Pékin : le projet des nouvelles routes de la soie, outre les infrastructures de transport, les crédits, le business, c’est aussi un nouveau type de relations internationales qui passe par le développement des échanges entre les hommes et doit profiter au monde entier.

Faisons un état des lieux du projet chinois des routes de la soie, qui va bien au-delà de l’objectif premier de connecter l’Asie à l’Europe. Aujourd’hui, Pékin fait des deals avec le monde entier. Du rachat du port d’Athènes au métro éthiopien d’Addis-Abeba, la Chine place des pions sur tous les continents avec un objectif : réinventer une nouvelle forme de mondialisation où Pékin est au centre et impose son modèle. Mais ce projet a aussi ses limites. Sans plus attendre, commençons à nous déplacer sur le grand Monopoly de Xi Jinping.

Les nouvelles routes de la soie revendiquent l’héritage historique des anciennes voies commerciales qui, dès le 2e millénaire avant notre ère, partaient de l’empire du Milieu vers l’Orient et l’Europe pour acheminer les trésors chinois, dont la soie. Traduit en anglais par « Belt and Road Initiative », ce projet est donc un ambitieux programme de modernisation des infrastructures existantes, routières et ferroviaires, à travers l’Asie Centrale, la Russie et le Moyen-Orient.

Ces dernières années, des liaisons ferroviaires hebdomadaires relient la Chine à l’Europe jusqu’à la Grande-Bretagne, de Wuhan à Londres en passant par Duisbourg. Le trajet dure 15 jours, soit moitié moins que par la mer.

Ces routes est-ouest permettent à la Chine de commercialiser ses productions et d’implanter le long de leurs tracés d’importantes infrastructures industrielles et de centrales énergétiques.

Par exemple, la ville de Khorgos, à la frontière sino-kazakhe, inclut un port sec intégré et une zone économique spéciale.

L’implantation de ces infrastructures est souvent une des conditions de la rénovation des voies de transport. Elle ouvre à la Chine de nouveaux débouchés pour ses énormes capacités de production que ne lui offre plus son marché intérieur, notamment pour l’acier, le ciment ou l’aluminium.

Cette stratégie, le gouvernement de Xi Jinping ne l’applique pas qu’à l’axe est-ouest. Il l’applique également en Asie, ce qu’on va voir maintenant.

Au Pakistan, la modernisation de la Karakoram Highway, qui culmine à 4 800 m, s’accompagne d’implantations de centrales électriques et d’un projet de voie ferrée. Dans ce couloir sino-pakistanais qui relie la ville de Kashgar, dans la province du Xinjiang, au port de Gwadar, au Pakistan, l’enjeu est de renforcer la coopération sino-pakistanaise dans les domaines clés du transport et de l’énergie, et d’offrir à la Chine un accès sur la mer d’Arabie.

L’amélioration de la connectivité entre les routes maritimes, sur lesquelles nous reviendrons, et la Chine, justifie également les travaux entrepris au sein des deux autres couloirs terrestres de la région : celui qui doit relier le Yunnan à Singapour à travers le Laos, la Thaïlande et la Malaisie, et celui qui doit relier la ville de Kunming au port birman de Kyaukpyu sur le golfe du Bengale.

Une voie ferrée devrait s’ajouter aux oléoducs et aux gazoducs en service entre les deux villes depuis 2013. Ces équipements permettent d’acheminer près de 22 millions de barils de pétrole et 12 milliards de mètres cubes de gaz par an vers la Chine.

Europe, Asie, le grand projet chinois des routes de la soie se développe de la même manière en Afrique, on va le voir maintenant.

Riche en matières premières, le continent africain intéresse grandement Pékin qui investit massivement dans certains pays, et construit des voies ferrées, notamment entre Djibouti et Addis-Abeba et entre Mombassa et Nairobi.

Nous venons de voir le volet investissement terrestre des routes de la soie. Nous allons voir à présent comment cette stratégie de contrôle par l’investissement s’applique aussi le long des routes maritimes.

C’est notamment le cas le long de la principale route entre la Chine et l’Europe, qui traverse l’océan Indien, la mer Rouge et la mer Méditerranée. Pékin a pris des intérêts importants dans les infrastructures portuaires par le biais des sociétés China Merchants Group et Cosco.

En Europe, on se souvient de l’émotion provoquée par l’acquisition via Cosco de 51% des parts du port grec du Pirée, en 2016. Une opération financière colossale : 368 millions d’euros qui permettaient à l’époque à Athènes d’éponger sa dette publique. Le Pirée qui n’est pas le seul port européen, désormais, administré par la Chine. Bilbao, Valence, Savone, Zeebruges, sont aussi sous le contrôle de Cosco.

Le long des autres axes maritimes, Pékin n’est pas en reste. Notamment le long des côtes de l’océan Pacifique. Pékin a investi dans plusieurs pays considérés comme le jardin des États-Unis, et prend peu à peu le contrôle de ports importants, comme celui de Chancay au Pérou.

Et puis, fonte des glaces aidant, Xi Jinping table également sur l’ouverture de la voie arctique. Permettant de gagner jusqu’à 40% de temps de trajet, cette route n’est encore accessible que quelques mois de l’année. Pékin investit déjà au Groenland, dont la position deviendrait stratégique sur ce nouvel axe.

Il apparaît d’après les données que l’on est bien loin, désormais, des anciennes routes de la soie. L’Afrique et l’Amérique latine, d’abord marginales dans le projet, tiennent aujourd’hui une place importante dans le Monopoly chinois qui se joue désormais à l’échelle de l’ensemble du monde.

À ces projets matériels des routes de la soie, les chemins de fer, les ports, les canaux et autres infrastructures, s’ajoute la coopération immatérielle avec notamment ce qu’on appelle le « soft power », dont on parlera. On va d’abord s’intéresser au volet financier des routes de la soie qui placent, de fait, sous dépendance chinoise ces pays qui bénéficient des crédits de Pékin.

Aujourd’hui, ils sont 138 pays à avoir rejoint les nouvelles routes de la soie via divers accords bilatéraux. Les fonds nécessaires à la mise en oeuvre du grand projet chinois donnent le vertige. Officiellement, la Chine compte y investir plus de 1 000 milliards de dollars sur 10 ans.

Mais ces financements se font par le biais de prêts et non pas de dons. Or les prêts octroyés par la Chine, à travers les banques chinoises, mettent les pays contractants dans une relation de dépendance à l’égard de la Chine, ce qui pousse à relativiser la philosophie gagnant-gagnant mise en avant par Xi Jinping.

Ainsi, la Thaïlande, en 2016, a renoncé à l’offre chinoise de financement de la voie ferrée reliant sa frontière nord-est à Bangkok, le deal étant jugé trop défavorable aux Thaïlandais. De même, la Tanzanie bloque depuis 2 ans les travaux du port de Bagamoyo. Elle a dressé un ultimatum à Pékin lui intimant d’accepter ses conditions ou de quitter le pays.

D’autres critiques sont formulées : le fait que le recours fréquent à de la main-d’oeuvre chinoise importée limite les créations d’emplois locales. Un argument valable au Pakistan où, dans le port de Gwadar, la moitié de la main-d’oeuvre était chinoise. Mais pas en Ethiopie où la Chine a employé 5 000 ouvriers éthiopiens pour la construction de la voie ferrée reliant Addis-Abeba à Djibouti.

On reproche également à la Chine d’avoir imposé certains projets surdimensionnés ou sans pertinence pour les pays concernés. C’est le cas de la voie express Kampala-Antebbe en Ouganda, dont les 500 millions de dollars auraient sans doute pu être utilisés de manière plus utile à l’économie locale. Ou encore la voie ferrée traversant le Laos, dont la construction aurait coûté 6 milliards de dollars, soit plus du tiers du PIB du pays, alors que, très probablement, y transiteront essentiellement des matières premières à destination de la Chine.

Et sur le volet environnemental, les tracés des nouvelles routes de la soie affecteraient 265 espèces menacées comme les antilopes, les tigres et les pandas géants.

Les centrales hydroélectriques, comme sur le Mékong, entraîneraient des dommages inestimables pour les ressources halieutiques. Sans parler des projets de déforestation, comme à Bornéo, qui entraîneraient des risques de glissements de terrains et inondations notamment.

Selon l’Institute of International Finance, 85% des projets des routes de la soie sont à l’origine de fortes émissions de gaz à effet de serre.

Alors, pour redorer son blason, la Chine a recours à des actions qui relèvent du « soft power » : en Europe, la Chine implante dans de nombreux pays des centres Confucius qui diffusent la langue et la culture chinoise. La Chine a aussi investi dans des équipes de football.

La Chine est de plus en plus présente dans les organisations internationales comme l’Organisation Mondiale de la Santé dont elle pourrait devenir le premier État contributeur si les États-Unis confirmaient le retrait voulu par Donald Trump. (Les informations de cet article datent d’octobre 2020)

Voilà pour cet état des lieux des routes de la soie, projet phare de la Chine du XXIe siècle qui place ses pions sur tous les continents et dans tous les domaines. Sauf qu’aujourd’hui, Xi Jinping rencontre des difficultés. Pékin, pour la 1re fois depuis des décennies, a renoncé à se fixer un objectif de croissance en 2020, reconnaissant que le redémarrage de son économie après la crise du coronavirus sera un processus lent et difficile.

Pour cet article, on s’est appuyé sur cet ouvrage dirigé par F. Lasserre: Les Nouvelles Routes de la Soie. (Disponible dans la bibliothèque de ce site).

Merci et bonne recherche!

Ravi de vous retrouver pour cet article.

Cette photo prise en Afrique montre un équipement très courant là-bas : des panneaux solaires associés à une batterie. Ces kits permettent à des habitants de villages non reliés au réseau électrique de s’éclairer, charger leurs téléphones, aller sur Internet…

Pour les plus optimistes, l’abyssal chantier de l’électrification du continent africain pourrait être résolu par la théorie dite du « saute-mouton » : l’Afrique passerait à l’étape des énergies renouvelables, sans passer par celle des lignes électriques. D’ici là, les inégalités d’accès à l’électricité restent flagrantes. Regardez comment!

La nuit en Afrique, les lumières de la ville ne scintillent pas pour tous. Regardons ces images de la NASA qui montrent les lumières artificielles la nuit. L’Afrique est le continent le moins électrifié de la planète.

Les populations d’Afrique du Nord sont presque toutes reliées à un réseau national, mais en Afrique subsaharienne, sauf en Afrique du Sud, la moitié de la population n’a accès à aucun service électrique.

Un sous-équipement d’autant plus frappant que d’autres réseaux se sont développés très rapidement, comme la téléphonie mobile: 80% de la population est équipée.

Le nombre de foyers possédant l’électricité a largement augmenté entre 1990 et aujourd’hui, mais il reste encore nettement inférieur à la moyenne mondiale. Seuls 45% des foyers éthiopiens possèdent l’électricité. 35% en Somalie, ou 11% au Burundi où seulement 2 villes, Bujumbura et Gitega, sont pourvues d’un réseau municipal.

La consommation électrique est en moyenne de 500 kWh par personne en Afrique subsaharienne, alors qu’elle atteint 4 000 kWh en Chine, 6 000 en Europe, 13 000 aux Etats-Unis, et 15 000 au Canada ou au Qatar.

Or, l’accès à l’énergie électrique est fortement corrélé au développement économique. On voit ici que les pays les moins électrifiés sont aussi ceux où les populations en situation d’extrême pauvreté sont les plus nombreuses. Cette corrélation s’explique par l’alimentation nécessaire au fonctionnement des machines de production, mais aussi par la capacité à s’éclairer après le coucher du soleil, et donc à augmenter le temps consacré aux activités productives. L’accès à l’électricité permet également le fonctionnement des centres de soins, le respect de la chaîne du froid. Il facilite enfin l’accès à l’information et l’éducation, et simplifie la vie ménagère.

Quant aux capacités de production électrique, les pays d’Afrique du Nord et d’Afrique australe ont des capacités de production proches des moyennes mondiales, basées surtout sur les énergies fossiles, et pour une petite part sur le nucléaire en Afrique du Sud. Les autres pays de l’Afrique subsaharienne ont des capacités plus limitées et dépendent davantage de l’hydroélectricité.

Si l’on exclut le cas sud-africain, 80 gigawatts peuvent être produits par les centrales subsahariennes, pour un milliard d’habitants, alors que la France, par exemple, a une capacité maximale de 130 GW pour 67 millions d’habitants.

Comme l’illustre cette photo, la situation énergétique de l’Afrique subsaharienne reflète la difficulté des Etats post-coloniaux à porter de grands projets d’aménagement du territoire.

Les réseaux électriques, principaux et secondaires, se sont focalisés sur les capitales, centres névralgiques des nouveaux pouvoirs, au détriment des zones rurales. L’immensité des territoires de la zone sahélienne et d’Afrique centrale rend, qui plus est, très coûteux le maillage du territoire. Alors que 63% des Africains vivent en dehors des villes, moins de 10% du territoire est couvert par les réseaux de distribution.

Dans les grandes agglomérations, l’extension des réseaux est facilitée mais est moins rapide que l’accroissement de la population. Dans les bidonvilles des grandes villes d’Afrique subsaharienne, moins de 10% de la population dispose d’un raccordement au réseau électrique.

Cette pénurie énergétique est accentuée par de nombreuses coupures de courant. Plus de 25 par mois au Nigeria.

Pour pallier le déficit des réseaux nationaux, ce sont souvent des solutions individuelles qui prévalent. Plus de la moitié des ménages nigérians possèdent un groupe électrogène. Ils fourniraient à eux seuls plus de 10 GW contre 6 GW disponibles via le réseau centralisé. C’est un cercle vicieux qui se met en place. Les populations se détournent des réseaux nationaux existants. Les factures impayées et les raccordements sauvages aggravent d’autant le déficit des entreprises électriques qui peinent à investir pour l’entretien et le développement du réseau.

Dans la zone subsaharienne, seuls les Seychelles et l’Ouganda parviennent à l’équilibre financier de leurs compagnies électriques. La moitié des pays de la zone couvrent à peine leurs frais de fonctionnement. Et les autres, leurs compagnies électriques sont en déficit. Paradoxe : les populations qui ne sont pas raccordées aux réseaux nationaux dépensent souvent plus d’argent pour leur énergie que les populations raccordées, du fait de l’achat de kérosène ou de piles.

La situation électrique de l’Afrique illustre bien le dilemme entre des projets pharaoniques portés par les Etats et qui peinent à se concrétiser, et des solutions alternatives individuelles qui se déploient rapidement. Et il existe plusieurs scénarios. Nucléaire, hydroélectricité, énergie solaire, les ressources ne manquent pas.

Commençons par parler de l’énergie nucléaire. L’Afrique du Sud est le seul pays à posséder des réacteurs sur le continent. Mais le Ghana, le Kenya, le Niger, le Nigeria et le Soudan ont tous fait part à l’Agence internationale de l’énergie atomique de leur volonté de développer l’énergie nucléaire, et envisagent de signer des accords avec des entreprises chinoises, russes, canadiennes, françaises, coréennes. Malgré les risques liés au nucléaire, cette énergie est d’autant plus attractive que l’Afrique possède près de 20% des réserves mondiales d’uranium, principalement situées en Afrique du Sud, en Namibie et au Niger.

L’hydroélectricité représente aussi un potentiel énergétique colossal. Le Nil, le Congo, le lac Tchad et ses affluents, et le fleuve Niger sont les 4 grands bassins hydrologiques de l’Afrique. Les cours d’eau pourraient produire 1 800 térawatts-heure chaque année, selon l’Agence internationale de l’énergie, et couvrir à eux seuls la plupart des besoins du continent.

En République démocratique du Congo, dont 99% de l’électricité provient de barrages existants, le projet Inga prévoit d’ajouter aux centrales déjà existantes un nouveau barrage d’une capacité de 42 GW, le Grand Inga, ce qui en ferait le générateur hydroélectrique le plus puissant au monde. Il pourrait fournir de l’électricité jusqu’en Egypte, en Namibie et en Afrique du Sud. Mais le lancement de ce projet pharaonique qui reviendrait à 80 milliards de dollars est constamment retardé. Aux problèmes techniques s’ajoute l’instabilité politique de la RDC qui décourage les investissements étrangers.

En Ethiopie, le remplissage du barrage Renaissance, sur le Nil bleu, a, lui, déjà commencé. Cela engendre de vives tensions avec l’Egypte, en aval, dont l’agriculture dépend des eaux du Nil. L’Egypte exige que le réservoir soit rempli très progressivement, sur 12 ans, alors que l’Ethiopie, elle, souhaite exploiter au plus tôt ses pleines capacités et le remplir en 4 ans pour qu’il fournisse de l’électricité à 50 millions d’Ethiopiens.

Et c’est bien sûr l’énergie solaire qui présente le potentiel le plus considérable et est encore très largement sous-exploité. La région subsaharienne est parmi les plus irradiées au monde. La plupart des pays de la région a une capacité supérieure à 2000kWh/m2/an, soit presque 2 fois plus que l’Allemagne. Or le parc photovoltaïque allemand a une capacité de 49 GW contre seulement 4,5 pour l’Afrique subsaharienne.

De grands projets de centrales photovoltaïques sont à l’étude ou déjà en service, comme celle de Garissa au Kenya. Mais là encore, le déploiement de l’énergie solaire centralisée est limité par la capacité des réseaux à distribuer l’électricité produite. Le solaire et l’éolien représentent seulement 2% du mix électrique de la région.

Pour les énergies renouvelables aussi, des solutions locales ou individuelles suppléent les faiblesses des infrastructures nationales et continentales. Ainsi, le marché des kits solaires se développe rapidement dans les zones rurales. Ces systèmes individuels permettent d’alimenter de petits appareils électriques. Via un téléphone portable, le client achète des « jours lumière », et rembourse progressivement l’achat du matériel selon un principe de leasing. Au Kenya, un million de ces kits ont été vendus au 2d semestre 2019, et en Ethiopie, plus de 700 000.

Vous le voyez sur cette carte proposée par l’Agence internationale de l’énergie, 3 axes se profilent donc pour électrifier l’Afrique subsaharienne:

• en bleu, l’extension des réseaux centralisés vers des zones urbaines et de productions industrielles,
• en orange, des mini-réseaux autonomes alimentés par des petites centrales,
• et en vert, des générateurs individuels pour les populations les plus isolées.

Cette dernière décennie, les bonnes volontés pour électrifier l’Afrique n’ont pas manqué. On rappellera l’objectif de développement durable numéro 7 de l’ONU qui vise l’accès universel à une électricité durable et abordable d’ici à 2030. Il est certain que le marché africain du solaire photovoltaïque a de beaux jours devant lui et que les investissements s’y font à un rythme effréné. Si on ne peut nier que l’électrification du continent progresse, ces progrès sont lents, et l’Afrique subsaharienne semble rester inexorablement dans l’ombre.

« Gestion des déchets et production d’électricité en Afrique », c’est le titre d’une étude de l’IFRI, à retrouver sur le site de l’IFRI.

Merci à vous et bonne recherche!

Merci d’être sur cette page. Nous démarrons cet article à Paris, sur les Champs-Elysées, avec la photo du défilé militaire du 14 juillet, ou comment la célébration de la prise de la Bastille en 1789 est progressivement devenue fête militaire, notamment à partir de 1880, le président de l’époque, Jules Grévy, souhaitant mettre en scène le redressement de la France après sa défaite contre l’Allemagne.

« La France ne peut être la France sans la grandeur », a écrit le général de Gaulle dans ses « Mémoires de guerre ». Cette grandeur française est un thème récurrent dans les discours des candidats à l’élection présidentielle, et la figure du Général est souvent invoquée.

Nous avons donc voulu évaluer la juste place de la France dans le monde du XXIe siècle. Economie, militaire, diplomatie, « hard », « gold » et « soft power » : voici la France, entre puissance et peur du déclin.

Depuis la fin de la 2de Guerre mondiale, la France est parvenue à maintenir son rang sur la scène internationale. Elle est l’un des cinq membres permanents du Conseil de sécurité de l’ONU, comme les USA, la Chine, la Russie et le Royaume-Uni.

Comme ses 4 partenaires, elle dispose de l’arme nucléaire, d’où une place prépondérante dans la géopolitique mondiale, même si, avec 67 millions d’habitants, la France pèse peu face au 1,4 milliard de Chinois ou face aux 332 millions d’Américains.

Si l’on regarde le PIB à présent, la France est également loin derrière les Etats-Unis ou la Chine, mais elle se classe tout de même en 7e place, derrière l’Allemagne, 4e, le Royaume-Uni et l’Inde.

La France, c’est aussi une économie qui continue d’attirer, avec dans le top 5 des pays investisseurs: les Etats-Unis, l’Allemagne, le Royaume-Uni, l’Italie et les Pays-Bas.

Autre caractéristique de l’économie française, sa dette. La dette publique française a atteint 115% du PIB en 2020, là où l’Allemagne est parvenue à rester sous la barre des 70%.

Berlin fait également mieux que Paris en termes de balance commerciale. La France a accusé en 2020 un déficit de 64,7 milliards d’euros, là où l’Allemagne est parvenue à un excédent de 183,2 milliards. Un déficit commercial qui s’accumule depuis 20 ans, et qui s’explique en partie par le recul du secteur industriel, qui est passé de 17,5% du PIB en 1995 à seulement 11% en 2019.

La France reste pourtant une puissance industrielle dans des secteurs clés comme l’automobile, l’agroalimentaire, le BTP, l’aéronautique, avec Airbus, ou encore l’énergie.

Avec ses 56 réacteurs en activité, la France est ainsi une grande puissance nucléaire civile. Cette dynamique industrielle hexagonale s’appuie sur les 54 pôles de compétitivité lancés en 2004, qui permettent de favoriser l’innovation dans des secteurs spécialisés, comme c’est le cas pour la Cosmetic Valley, située entre Chartres et Orléans.

Le marché du luxe français se porte très bien. 4 groupes tricolores figurent dans le top 10 des plus grandes entreprises mondiales du secteur. LVMH arrive en tête, puis Kering, 2e, L’Oréal, 5e, ou encore Hermès, à la 9e place.

Mais à côté du très haut de gamme, l’industrie textile est en déclin en France, notamment dans la région historique des Hauts-de-France. En 2021, le textile regroupe encore 2 150 entreprises, qui emploient plus de 60 000 personnes, mais en 30 ans, ses effectifs ont été divisés par 7.

En réalité, l’économie française est aujourd’hui dominée par le secteur des services, qui représente 80% du PIB. Aux côtés des leaders mondiaux dans le domaine de la banque, des assurances ou de la grande distribution, on trouve le tourisme, qui représente 10% du PIB. Le climat océanique hexagonal, si apprécié des touristes, est également favorable à l’agriculture française, qui représente 3,6% du PIB et 5,6% de l’emploi, et fait ainsi de la France la 1re puissance agricole européenne et le 6e exportateur mondial.

Enfin, territorialement, la France a un atout majeur : elle est bien plus vaste que le seul Hexagone, Corse comprise. En plus de ses 5 départements et régions d’outre-mer, avec la Réunion et Mayotte dans l’océan Indien, mais aussi la Guadeloupe, la Martinique et la Guyane, la France est également souveraine sur des collectivités comme St-Pierre-et-Miquelon, St-Barthélémy et St-Martin, mais aussi dans le Pacifique, avec la Polynésie française, Wallis-et-Futuna et bien sûr la Nouvelle-Calédonie qui, en décembre 2021, a voté contre l’indépendance.

A ces territoires, on peut ajouter les zones dédiées à la science que sont les Terres australes et antarctiques française. La France possède ainsi le 2e plus vaste domaine maritime au monde, après les Etats-Unis.

La France dispose donc d’atouts considérables, diplomatiques, militaires, économiques ou scientifiques, qui lui permettent de jouer un rôle important sur la scène internationale, mais cette place est menacée par la montée en puissance de nouveaux acteurs : Chine, Inde, notamment.

Pour continuer de peser dans ce monde multipolaire, la France compte sur l’Union européenne. Regardons!

La France exerce actuellement la présidence tournante du Conseil de l’Union européenne. L’Union est une nécessité pour la France, qui y fait 54% de ses échanges. La présidence Macron a plaidé en 2021 pour une plus grande intégration économique avec le plan de relance post-Covid-19 de 750 milliards d’euros, un mécanisme de soutien historique, rendu possible par l’intensité du dialogue entre Paris et Berlin. La France plaide aussi en faveur d’une Europe autonome au niveau stratégique, en termes technologiques comme militaires.

Voyons justement comment la France se positionne militairement dans le monde! Aux bases situées dans l’Hexagone et en outre-mer s’ajoutent des bases situées en Afrique et aux Emirats arabes unis, ainsi qu’un déploiement maritime en Atlantique Nord, dans le golfe de Guinée et dans l’océan Indien. S’agissant de la marine de guerre, la France se place au 7e rang en termes de tonnage, et elle est l’une des 5 flottes mondiales à disposer d’une dissuasion nucléaire embarquée permanente. En 2020, l’armée française comptait 205 700 personnels militaires, dont 30 000 étaient déployés en opération, avec 400 militaires dans les pays baltes dans le cadre de l’OTAN, 720 casques bleus, notamment au Liban, en RDC ou en République centrafricaine, 600 militaires pour l’opération Chammal en Syrie et en Irak, et 5 100 soldats dans le cadre de Barkhane, répartis entre la Mauritanie, le Mali, le Burkina Faso le Niger et le Tchad.

Un dispositif militaire qui a été revu à la baisse par le président Macron à partir de juillet 2021, avec la fermeture de 3 bases dans le nord du Mali, à Tessalit, Kidal et Tombouctou.

Puis en février 2022, soit 9 ans après le début de l’opération Serval pour repousser les forces djihadistes, Paris a confirmé le désengagement progressif des forces françaises installées au Mali. Car la présence française en Afrique est remise en cause par de nombreux acteurs, qui entendent bien prendre le relais des anciennes puissances coloniales.

Ainsi les Chinois ont des accords militaires avec 6 pays d’Afrique. On peut ajouter à cela les manoeuvres russes, qui ont déployé des mercenaires du groupe Wagner en République centrafricaine, en Libye, au Soudan, au Mozambique, et qui, début 2022, étaient en déploiement au Mali.

En 2021, c’est aussi et surtout dans la zone indo-pacifique que la France veut convaincre qu’elle demeure une puissance mondiale. Face à l’émergence des géants chinois et indien, elle a commencé à se rapprocher de l’Inde et de l’Australie dans les années 2000 pour tenter de construire un axe stratégique Paris-New Dehli-Canberra.

Mais la crise diplomatique déclenchée en septembre 2021 par la création de l’alliance AUKUS entre Washington, Canberra et Londres contre Pékin, et l’annulation du contrat de livraison à l’Australie de 12 sous-marins français a bouleversé la donne régionale et les ambitions de Paris. Car l’Indo-Pacifique abrite 93% de la zone économique exclusive française, et 1,6 million de ressortissants, répartis dans les divers territoires d’outre-mer. Un rapprochement avec l’Inde est toujours envisagé. Dehli a ainsi acquis 36 avions de combat Rafale du groupe Dassault en 2016, pour un montant de 7,87 milliards d’euros, et Paris compte sur le renforcement de partenariats déjà engagés avec le Japon, la Nouvelle-Zélande, le Vietnam ou l’Indonésie pour tirer son épingle du jeu.

La France est sans doute devenue, comme le disait Giscard d’Estaing, « une grande puissance moyenne de rayonnement mondial ». Atouts militaires et diplomatiques, dynamisme économique plus fragile, influence culturelle et linguistique encore bien réelle : la France dispose toujours des attributs de la puissance, mais doit désormais, dans un monde multipolaire, compter sur l’Union européenne et sur le multilatéralisme pour continuer de peser.

Enfin la France a un handicap qui lui est propre : une défiance envers les institutions et une peur de l’avenir bien plus élevée que dans les autres pays européens de niveau économique comparable.

Pour aller plus loin, cet ouvrage collectif, qui revient également sur ce penchant très français pour l’autodénigrement. (voir la biblithèque de ce site)

Bienvenue dans ce nouvel article. Cette photo, datant de 2009, montre Vladimir Poutine visitant une exploitation agricole dans la région de Krasnodar, l’une des plus chaudes de Russie, disposant des terres parmi les plus fertiles du pays. Si Poutine pose dans ce champ, c’est qu’il a fait du blé une arme géopolitique.

Après le « soft power » et ses guerres d’influence via la culture et l’information, voici donc le « food power », l’arme alimentaire. Le blé, céréale essentielle, a de tout temps été un outil de puissance, des Grecs de l’Antiquité aux Allemands du nazisme, sans oublier le plan Marshall des Américains après 1945. Voyons comment le blé contribue à redonner de la puissance à l’ex-URSS. Sortons nos cartes!!!

La production de blé est inégalement répartie sur le globe, restant concentrée dans très peu de pays. 85% de la production mondiale proviennent de 10 puissances, dont les Etats-Unis, la Russie, l’Union européenne, la Chine, situées en majorité dans l’hémisphère Nord.

En parallèle, de nombreux Etats dépendent de leurs importations pour nourrir leurs populations, comme en Afrique du Nord, l’Egypte et l’Algérie, et globalement tout le sud du bassin méditerranéen.

Ce décalage Nord-Sud met le blé au coeur d’enjeux stratégiques majeurs, et ce depuis des siècles, comme nous allons le voir.

Durant l’Antiquité, le blé est déjà essentiel pour les Grecs. La cité d’Athènes, à la puissance navale et commerciale inégalée, connaît un grave problème : la production de blé est insuffisante pour nourrir une population qui atteint 250 000 habitants au Ve siècle av. J.-C. Pour éviter les révoltes, il faut s’approvisionner ailleurs : Sicile, Syrie, Egypte, et pourtours de la mer Noire deviennent les greniers à blé d’Athènes.

Autre exemple parmi ces régimes dont les ambitions de puissance exigent de sécuriser l’approvisionnement en blé : le Troisième Reich. Les nazis ont l’idée de conquérir des terres pour nourrir le peuple et notamment les soldats. L’opération Barbarossa, en 1941, en est l’illustration. En attaquant l’Union soviétique, Hitler vise autant les matières premières que Moscou. Objectif : les mines de charbon du Donbass, mais surtout l’Ukraine et son blé.

Le blé comme socle des Etats pour asseoir leur puissance, c’est aussi ce que raconte l’Amérique de la guerre froide. En 1945, les Etats-Unis sont devenus un géant agricole, grâce à leur plaine céréalière. Ils commencent à exporter leur surplus de blé. Washington comprend vite que le blé peut servir ses intérêts dans la rivalité Est-Ouest naissante. Dans cette lutte d’influence, l’aide alimentaire va servir à freiner l’expansion soviétique. Durant la guerre froide, l’exportation du blé a permis d’accompagner le déploiement militaire américain d’Asie du Sud au Moyen-Orient, et en Europe via le plan Marshall, où l’aide alimentaire renforcera la cohésion des alliés des Etats-Unis. Une réussite qui va pousser l’Europe à redevenir une puissance agricole.

Et la France ? Après la Seconde Guerre mondiale, l’agriculture est exsangue. Paris doit importer les 2/3 du blé. Le plan Marshall, puis la PAC, politique agricole commune, permettent de rebâtir une agriculture plus moderne et plus productiviste. Dès la fin des Trente Glorieuses, l’autosuffisance est atteinte, grâce à la Beauce, principal grenier à blé. La France devient exportatrice.

Alors, en 2022, où en est le continent européen ? France et Allemagne sont en tête. Avec 13,4 millions de tonnes par an vendues à l’étranger, la France exporte 50% de sa production, en Afrique du Nord et en Chine surtout, étant l’un des rares pays contribuant à la sécurité alimentaire mondiale.

Ce marché du blé est donc dominé par l’Occident depuis 1945. Mais l’Union européenne et les Etats-Unis sont détrônés par la Russie, acteur clé de cette géopolitique du blé.

En moins de 20 ans, la Russie a pris la tête du classement mondial d’exportation de blé. Une 1re place que la Russie doit à ses terres noires du sud-ouest, réinvesties sur le plan agricole après le démantèlement des fermes collectivistes, kolkhozes et sovkhozes. Plus à l’est, avec le changement climatique, le dégel de la Sibérie pourrait élargir la surface agricole russe. Faisant de l’agriculture un atout de puissance, Vladimir Poutine a rêvé de créer une OPEP du blé avec l’Ukraine et le Kazakhstan, pour renforcer leur poids. A eux trois, ils représentent 20% des exportations mondiales de blé. Mais la crise russo-ukrainienne a éloigné cette perspective.

Alors, comment la Russie de Poutine utilise ses exportations de blé pour étendre son influence géopolitique ? Elle exporte son blé notamment en Egypte, en Libye, en Turquie, en Iran, mais aussi en Syrie. En 2016, Poutine a volé au secours de son allié Bachar el-Assad. En plus d’une couverture aérienne, il lui a offert du blé en quantité. Objectif : fournir en pain la population des zones contrôlées par le gouvernement el-Assad.

D’ailleurs, dans la guerre en Syrie, un enjeu majeur est méconnu : le contrôle des terres agricoles. Moins médiatique que l’or noir, le contrôle du blé a été crucial dans l’implantation de l’Etat islamique, dans les régions céréalières du nord-est de la Syrie et du nord de l’Irak. Pour Daech, le blé a été une arme de guerre. En 2015, il lui rapporte 200 millions de dollars, soit 12% du budget de l’organisation terroriste. Derrière le pétrole, qui représente 25% de ses ressources financières.

Restons au Moyen-Orient, jusqu’à l’Afrique du Nord. Avec 30 millions de tonnes par an achetées à l’étranger, c’est la région du monde qui importe le plus de blé. L’Egypte, l’Algérie et le Maroc sont les pays les plus dépendants de ces importations, d’où leur grande vulnérabilité. Ici comme au Moyen-Orient, l’eau est rare, les terres fertiles aussi, et la poussée démographique est forte. De 139 millions d’habitants en 1961 à 500 millions aujourd’hui. Les besoins alimentaires en produits agricoles ont été multipliés par 6 depuis les années 60. Aussi, dans ce Moyen-Orient, le blé agit en détonateur quand il vient à manquer ou que son prix explose. Souvenons-nous des printemps arabes en 2011. En 2010, les prix du blé avaient flambé : près de 300 euros la tonne.

Ceci a joué dans les soulèvements de 2011, en décuplant le rejet de l’autoritarisme et de la corruption des pouvoirs en place. Aujourd’hui, cette région importe majoritairement du blé de Russie.

En Algérie, la France et la Russie se livrent une intense bataille. La France y perd des parts de marché, passant de 5,6 millions en 2019 à 1,85 million de tonnes de blé en 2020, soit une baisse de plus de 60%. Le blé français subit désormais la concurrence des céréales russes, moins chères et de bonne qualité. En diversifiant ses importations, Alger veut s’émanciper de l’ancien colonisateur, qui avait beaucoup augmenté la production de blé à l’époque de l’Algérie française.

Pour terminer, intéressons-nous à la Chine. Avec 130 millions de tonnes par an, c’est le premier producteur mondial de blé. Le projet de puissance de Xi Jinping exige de sécuriser l’approvisionnement alimentaire. Mais cet objectif d’autosuffisance est de plus en plus inatteignable. En cause, l’explosion de consommation de blé des Chinois, dont le régime alimentaire s’est occidentalisé.

Pékin achète des céréales au Canada, à l’Union européenne, à l’Ukraine, ou à la Russie. Cette année, elle a importé 10 millions de tonnes de blé pour nourrir sa population, contribuant à la flambée des cours.

Fin de ce tour du monde du blé, céréale cruciale, devenue arme de « food power ». Le blé intéresse aussi les boursicoteurs, avec un marché volatil. Ainsi, la valeur du blé peut fluctuer du simple au double. Et beaucoup d’agriculteurs surveillent autant leurs champs que la bourse.

L’explosion de la bulle Internet au début du XXIe siècle a poussé le monde de la finance vers des valeurs traditionnelles, comme les céréales. Le blé est entré dans l’économie de marché, pour le meilleur et le pire.

L’article a été préparé à l’aide de « Terres, pouvoirs et conflits » livre de Pierre Blanc. (Disponible sur la bibiothèque de ce site)

Merci de vous retrouver sur cette page pour cet article concernant la démocratie. Démarrons avec cette image du 1er mars 2022, les eurodéputés n’oublieront pas l’intervention poignante en visioconférence de Volodymyr Zelensky le dirigeant ukrainien rappelant aux européens quelques jours après le début de l’offensive russe sur l’Ukraine qu’il s’agissait d’une guerre pour défendre la démocratie, le droit, les libertés, une guerre qui par conséquent devrait concerner est impliquer le monde entier.

Alors bien sûr avant que ne démarre cette guerre, on ne pouvait pas dire de la démocratie ukrainienne qu’elle était une démocratie parfaite à cause du maintien de certaines élites de l’ancien régime et de la corruption mais cette démocratie ukrainienne en devenir constituait déjà malgré tout un modèle alternatif précieux aux portes de la russie autocratique de Vladimir Poutine.

Alors précisément, on a voulu tenter un état des lieux de la démocratie dans le monde: face aux autocrates que pèsent les démocrates? pourquoi l’enjeu démocratique est il un enjeu crucial du monde qui vient ?

Sortons nos cartes …

En 2021 dans le monde selon the Economist Intelligence Unit on recense:

• 21 démocratie véritable: Canada Islande Norvège Suède ou Finlande.
• 53 démocraties défectueuses. Cette catégorie englobant des pays très différents, certains habituellement considérés comme véritablement démocratiques exemple le Portugal pénalisé par son faible taux d’adhésion à des partis (syndicats ou associations) ou encore par son fort taux d’abstention aux élections. Cette catégorie comprend aussi à l’autre bout du spectre des pays tels la Hongrie avec la démocratie illibérale de Viktor Orban qui impose un renforcement de l’état et une diminution des libertés.
• 34 trente quatre régimes dits hybrides qui partagent certaines caractéristiques avec les démocraties comme les élections mais bafouent l’état de droit et les libertés individuelles.
• 59 régimes autoritaires parmi lesquels la Russie où il n’y a pas d’opposition et où Vladimir Poutine a fait changer la constitution de façon à pouvoir se maintenir au pouvoir jusqu’en 2036. Depuis la guerre en ukraine, le terme de dictature est de nouveau utilisé pour qualifier l’état poutinien.

L’évolution de ces chiffres montre un vrai recul de la démocratie. Ainsi nous sommes passés de 8,4% de la population mondiale vivant dans des démocraties véritable en 2020 à 6,4% seulement 2021 est. Désormais 54,3 % de la population mondiale soit plus de la moitié de l’humanité vit dans des régimes autoritaires ou hybrides.

Nous vivons donc un moment de vulnérabilité démocratique après plusieurs décennies d’ascension de ce modèle. En effet, en remontant à la seconde guerre mondiale, on voit que celle ci marque en occident la victoire des démocraties contre le nazisme, un élan qui se poursuit dans la seconde moitié du 20e siècle d’abord en europe, Portugal et Grèce Espagne, les régimes autoritaires s’effondrent laissant place à des démocraties. Ensuite en Amérique du Sud, Argentine, Uruguay, Brésil puis en Asie, Philippines, Corée du Sud. Le modèle démocratique semble triompher entre 1988 et 1991 avec la fin de l’URSS: la constitution de nouveaux états en europe centrale et orientale qui adoptent pour la plupart les valeurs démocratiques de l’Union Européenne.

Toutefois les interventions américaines en 2001 en Afghanistan et en 2003 en Irak vont marquer l’échec de l’implantation de la démocratie par la force.

Autre désillusion démocratique: les printemps arabes. Si la chute de certains dictateurs tels Ben Ali en Tunisie, Kadhafi en Libye ou Moubarak en Egypte créé dans un premier temps l’espoir d’un événement démocratique, celui ci va être brisé par l’évolution politique de la région y compris en Tunisie après une première phase prometteuse de démocratisation.

Ce début de XXIème siècle marque donc l’arrêt de l’expansion des démocraties trente ans après leur triomphe marquée par la chute du mur de Berlin. Elles sont même dans une situation périlleuse d’une part à l’extérieur les tensions avec les régimes autoritaires ne sont pas sans rappeler la guerre froide, d’autre part le démocratie subissent des tensions intérieures et c’est ce qu’on va voir maintenant.

Car les démocraties sont par essence ouvertes à la contradiction, du coup elles peuvent être l’objet de critiques et de faiblesses. A cela s’ajoute le fait que les démocraties occidentales ont été fragilisées par un double mouvement de mondialisation et de désindustrialisation générateur d’un sentiment de déclin et de défiance populaire.

Regardez en France cette carte de 2013 qui présente un indice d’inégalités élaborée à partir de données compilant à parts égales chômage, pauvreté, absence de diplôme et familles monoparentales:

Regardez! Les zones en plus grande difficulé correspondent à celles du vote FN lors du premier tour de l’élection présidentielle de 2012.

Toujours en France, la défiance des peuples se manifeste aussi par l’abstention, laquelle contribue à fragiliser la démocratie.

En juin 2021, l’abstention lors des élections régionales atteint plus de 65%. A cela s’ajoute un sondage réalisé en octobre 2021 dans lequel 72% des français estiment que leur opinion n’est pas pris en compte par les dirigeants politiques. Ainsi, le mouvement des gilets jaunes en avait déjà été une illustration. La montée des extrêmes lors de l’élection présidentielle de 2022 en est une autre.

Cette radicalisation du débat public entraîne une légitimation croissante de la violence comme expression politique.

Le point culminant de cette violence à lui aux états unis avec l’invasion du Capitole le 6 janvier 2021 par les partisans de Donald Trump qui contestent l’élection de Joe Biden provoquant la mort de cinq personnes.

Les démocraties sont également menacées de l’intérieur par un risque de morcellement qui peut être le fait de mouvements séparatistes, d’ennemitié entre communautés religieuses ou de tensions autour de revendications communautaristes. Ainsi en Espagne, la volonté de sécession de la région catalogne a créé une crise institutionnelle autour de la question de la légalité d’un référendum d’autodétermination sans l’accord du reste du pays.

Evoquons maintenant un autre risque pour les démocraties: les circonstances exceptionnelles. Ainsi les attentats terroristes comme en France en 2015 ou plus récemment l’épidémie du Covid 19 dans le monde.

Dans ces situations, les gouvernements font face à une tension entre une demande impérieuse de sécurité et le respect des libertés. Une pandémie qui a aussi montré la rapidité avec laquelle les fake news et les théories complotistes se propagent par les réseaux sociaux, un phénomène d’autant plus inquiétant que ces réseaux sont une importante source d’information. Ainsi dans des pays comme le Chili, l’Argentine, la Grèce ou la Bulgarie, plus de 65 % des adultes s’informent sur ces réseaux.

Pourtant il existe un exemple positif d’intégration du numérique dans la vie démocratique, c’est celui de Taïwan. En effet, les 23,5 millions d’habitants peuvent interagir avec le gouvernement et l’administration par l’intermédiaire d’un portail officiel mis en place par le National Development Council non seulement pour les démarches administratives mais aussi pour se renseigner ou réagir à propos des lois en discussion ou en application et la gestion de la pandémie avec ces outils est souvent mise en avant comme un exemple de collaboration entre le gouvernement et la population. Malgré les lourdes menaces que la Chine fait peser sur l’île c’est un véritable laboratoire de la démocratie directe.

Regardons à présent les tensions externes: des tensions entre démocratie et régimes autoritaires qui ne sont pas sans rappeler la guerre froide. Toutefois il existe une différence majeure avec cette période à quelques exceptions près: ces nouveaux régimes autoritaires entendent participer à la mondialisation économique. Le meilleur exemple est celui de la Chine dont la montée en puissance a été accélérée par son entrée le 11 décembre 2001 dans l’Organisation Mondiale du Commerce.

Avec la Chine, le dogme occidental selon lequel la mondialisation économique conduite in fine à la mondialisation du modèle démocratique trouve ses limites. Le régime chinois reposant sur un parti unique, une absence de contre-pouvoir, une presse de propagande, des arrestations arbitraires et des camps de concentration pour les minorité ouïghoures. Par ailleurs, depuis 2013 et le lancement des nouvelles routes de la soie, la chine essaie aussi de diffuser ses valeurs notamment en Europe de l’Est.

Sur un plan économique tout d’abord, sa main mise passe bien sûr par les investissements dans les infrastructures mais la Chine détient aussi une bonne part de la dette de ces pays avec en 2018 20 % de celle de la Macédoine du Nord et 40 % de celle du Monténégro.

Sur un plan politique, Pékin met aussi en avant l’inefficacité de la démocratie européenne à ses yeux et la force de son modèle autoritaire censé assurer ordre et prospérité.

Par ailleurs, le 21e siècle offre aux régimes autoritaires une nouvelle arme: les nouvelles technologies. Grâce à elles, il est plus facile que jamais de s’immiscer dans les affaires des démocraties qui sont par nature plus ouvertes, de les espionner, d’en perturber le fonctionnement par le piratage informatique ou la production massive de fausses informations. Ainsi, selon le ‘Digital Defence Report’ entre juillet 2020 et juin 2021, parmi toutes les cyber attaques liées à des états, 58 % provenaient de la Russie et de fait, en février 2022 l’Ukraine a accusé la Russie de cyber attaques contre des sites militaires officielles et deux banques publics, celles ci ont eu lieu avant l’invasion russe.

Arrêtons-nous d’ailleurs pour terminer sur cette guerre toujours en cours depuis fin février 2022 et qui se joue aussi sur la défense de la démocratie et du respect du droit international.

L’assemblée générale de l’ONU a adopté le 2 mars 2022 une résolution pour sanctionner le recours à la force de la Russie contre l’Ukraine, résolution approuvée massivement par 141 pays, les cinq qui se sont opposées sont la Russie la Biélorussie la Corée du Nord l’Erythrée et la Syrie soit 5 dictatures, trente cinq se sont abstenus dont la Chine et l’on retrouve parmi ces abstentionnistes un certain nombre de régimes que notre carte de départ ne rangeait pas dans la catégorie des démocraties.

On l’aura compris, dans le monde des années 2020 la démocratie est menacée par des régimes autocratiques qui diffusent leurs modèles par tous les moyens militaires économiques numériques.

La guerre en Ukraine a réveillé les démocraties occidentales, dirigeants et nous autres citoyens qui avons parfois tendance à oublier ce que rappelait si bien l’ex-président tchécoslovaque Vaclav Havel dans son discours à la nation le 1er janvier 1990:

« Le meilleur gouvernement, le meilleur parlement et le meilleur président ne peuvent pas à eux seuls faire grand chose. La liberté, la démocratie, cela signifie d’abord et avant tout la participation et la responsabilité de tous »

Vous trouverez de nombreuses publications consacrées aux nouvelles pratiques démocratiques sur le site des chercheurs du think tank Terra Nova (tnova.fr)

Merci d’être sur cette page!!! pour cet article, notre photo du jour nous emmène en corée du sud voici le port de l’usiné hyundai récemment classée comme la plus grande usine automobile du monde. D’ici sort en effet chaque année un million cinq cent mille voitures.

Parler voiture au 21ème siècle donne de toute façon de vertige! Imaginez nous sommes 7 milliards et demi d’êtres humains et à nous tous nous possédons plus d’un milliard d’automobiles et en 2050 rappelez vous en bien: le nombre de voitures sur la planète pourrait doubler, un peu effrayant bien sûr quand on sait aujourd’hui que la voiture est en ville la première source de pollution et pourtant nous avons construit nos sociétés contemporaines sur le modèle suivant: le développement d’un pays entraîne le développement d’une classe moyenne qui entraîne le développement d’une industrie automobile. Aujourd’hui c’est au tour des pays du sud d’épouser ce modèle et la voiture ‘nous allons le voir’ est devenue ces dernières années un cas d’école de produits mondialisés.

Alors tout d’abord la voiture génère un business de première importance puisque le secteur représente à lui seul 9 % du commerce mondial.

L’automobile c’est donc aussi beaucoup d’emplois : environ 50 millions de personnes d’emplois directs est aussi indirects dans le monde, de la fabrication du moteur à la construction des routes. Dans les pays de l’Union Européenne par exemple cela représente 138 millions de salariés soit 6% de la population active c’est dire si cette activité stratégique pour les gouvernements qui cherchent à attirer ou à défendre dans leur pays les usines automobiles que vous voyez ici sur la carte.

Mais la voiture on le sait c’est aussi des émissions de CO2 responsables du réchauffement climatique et des émissions de gaz et de particules fines qui favorisent les maladies cardiovasculaires et respiratoires.

En somme la voiture est un condensé de notre société de consommation mondialisée et pour bien comprendre nous allons faire un peu d’histoire.

L’histoire industrielle de la voiture commence il ya un peu plus d’un siècle en 1908 dans la ville de détroit au bord des grands lacs américains. L’industriel Henry Ford invente la chaîne de montage et avec des gestes mécaniques et répétées, les ouvriers américains construisent la première automobile pour tous la ford 6. Dans cette première moitié du 20e siècle la voiture se démocratise et devient l’incarnation du rêve américain, réussite sociale et libertés individuelles triomphantes. L’Amérique produit du pétrole et des voitures à essence ce qu’on appelle les big three: Ford, General Motors et Chrysler dominent le marché mondial. En Europe l’industrie automobile se développe un peu plus tard en 1938 à la demande d’Hitler nait en Allemagne la voiture du peuple la Wolkswagen. Après la guerre cet emblème de la voiture allemande désormais surnommée coccinelle devient même dans les années 70 la voiture la plus vendue au monde.

Pendant les trente glorieuses l’industrie automobile prospère en Europe: l’Allemagne, la France, l’Italie, le Royaume-Uni ont chacun leur champion et leurs gigantesques ‘usines-cités’ comme celle de Renault à Boulogne billancourt en banlieue de Paris.

Le Japon avec Toyota est lui aussi dans la course: dans les années 60 son patron impose un nouveau modèle de production: le toyotisme basée sur la production à flux tendu. Les pièces détachées sont livrées chaque jour à l’ usine d’assemblage ce qui permet d’éviter la surproduction et les coûts de stockage. Aujourd’hui cette production qu’on appelle le juste-à-temps est devenue la norme.

Voyons maintenant à quoi ressemble le marché mondial en 2019 mais cette fois ci du point de vue des clients. Cette carte nous montre ce qu’on appelle le taux de motorisation c’est à dire le nombre de voitures par habitant dans chaque pays du globe, plus la couleur est foncée plus ce chiffre est élevé.

On le voit, les inégalités d’accès à l’automobile sont aujourd’hui très fortes. Aux états unis il y a près de 800 voitures pour 1000 habitants, l’Union Européenne et le Japon en compte 600 pour 1000 habitants, en Chine il n’y a que 140 automobile pour 1000 habitants tandis qu’en Inde on en dénombre seulement 19 pour mille.

Oui mais voilà depuis les années 1990 les pays émergents sont en plein rattrapage, l’Asie en tête. Avec l’essor des classes moyennes urbaines avides de prestige social, ces pays s’équipent désormais à grande vitesse.

Les chinois sont aujourd’hui les premiers acheteurs de voitures dans le monde, le parc automobile chinois a été multiplié par cinq en dix ans. Au fil des années les marques chinoises notamment geely bas au jaune changan et great wall ont gagné des parts de marché sur leurs concurrents étrangers avec le soutien actif du gouvernement. Pourtant wolkswagen arrivé très tôt en chine reste aujourd’hui leur marque préférée.

A Pékin avec ses 7 périphériques et ses 20 millions d’habitants les vélos ont cédé la place aux quatre roues modifiant profondément le paysage urbain.

Alors désormais c’est cet appétit des citadins chinois pour la voiture qui tire l’ensemble de la production mondiale. La chine produit près d’un tiers des véhicules construits chaque année dans le monde devant l’Union Européenne, l’amérique du nord, le japon et la corée du sud.

Alors regardons à présent le cas de l’inde, un autre marché en plein essor en particulier à New Delhi et dans les états les plus urbanisés de l’ouest et du sud du pays. En Inde, les constructeurs nationaux ont d’abord dominé le secteur avec la Tata Nano par exemple la petite voiture la moins chère au monde (1500 euros) qui a été lancée en 2008 par le célèbre groupe indien Tata Motors et qui a fait son succès. Mais victime de son image de voiture du pauvre la Tata Nano a aujourd’hui disparu du marché, elle a été remplacée par des modèles qui inspire davantage confiance aux indiens lamarre outils alto du grand groupe indien Marutti qui s’est allié au japonais Suzuki ou encore la Quid construite et vendue exclusivement en Inde par Renault.

En clair, on l’aura compris l’industrie automobile s’est profondément transformée ces dernières années, elle a multiplié alliance et rachat pour s’adapter aux récents bouleversements de la demande mondiale et notamment à cette nouvelle clientèle asiatique. En fait, c’est vraiment une nouvelle géographie de la voiture qui se dessine aujourd’hui qui se jouent toujours plus vous allez le voir des frontières. Par exemple, le français Renault pour jouer dans la cour des grands s’est allié avec le japonais Nissan et ensemble ils ont racheté le roumain Dacia et le coréen Samsung le russe Avtovaz avant de s’allier enfin un autre japonais Mitsubishi: Les mêmes pièces sont montées sur plusieurs modèles, ce qui permet des économies d’échelle. Et puis pour faire baisser les coûts de main d’oeuvre et éviter les taxes, les grands constructeurs ont délocalisé les usines hors de leurs frontières. Au Mexique par exemple les ouvriers des maquiladoras, ces usines exonérés de droits de douane situées juste de l’autre côté de la frontière avec les Etats Unis assemblent les modèles de Ford, Chrysler et General Motors à destination du marché américain. Leurs salaires sont quatre fois moins élevés qu’aux Etats Unis.

En Europe, la production s’est en partie déplacées vers l’est en Pologne en Slovaquie en République Tchèque en Slovénie en Hongrie et en Roumanie et vers le sud en Turquie et au Maroc essentiellement.

En france ce mouvement s’est accompagné de fermeture d’usines (vous les voyez ici) et de très nombreux plans de licenciements entre 2005 et 2010 : plus de cent mille emplois ont été détruits.

Alors à présent posons la question qui fâche l’industrie automobile la très polluante bagnole peut-elle devenir écolo ???

En 2018 l’industrie automobile a représenté 9 % des émissions mondiales de gaz à effet de serre. Alors que la prise de conscience de l’urgence climatique devient mondiale, les nouvelles normes d’émissions de CO2 obligent l’industrie à préparer le remplacement du moteur à essence ou diesel. Cette mutation technologique aura nécessairement un impact social. En Allemagne la grande puissance automobile européenne, les syndicats craignent la perte de dizaines de milliers d’emplois dans la prochaine décennie. La voiture électrique demande en effet moins de main d’oeuvre que les modèles thermiques.

La chine a déjà une bonne longueur d’avance en la matière, les chinois ont acheté plus de la moitié des véhicules électriques ou hybrides vendus dans le monde en 2018 et ils en produisent une grande partie. La chine est également le premier constructeur mondial de batteries lithium-ion devant le Japon et la Corée du Sud. Pékin a aussi la main sur un métal indispensable à la fabrication de ses batteries: le cobalt, grâce au contrôle d’importantes mines en République Démocratique du Congo, le premier producteur de cobalt.

Autre solution industrielle: une voiture alimentée par une pile à hydrogène. C’est le Japon qui domine aujourd’hui cette technologie encore coûteuse mais qui ne produit ni déchets ni pollution liée à l’exploitation minière.

Enfin à l’horizon 2040 ces voitures forcément plus propres, ce ne serons pas nécessairement nous qui les piloterons, ce seront des robots qui prendront le volant. En californie la Silicon Valley est ainsi devenu l’épicentre de la recherche sur ce qu’on appelle la voiture autonome avec des collaborations entre les plus grands constructeurs mondiaux et les géants du numérique.

Il existe enfin une autre option pour l’avenir, la meilleure: apprendre à nous passer de la voiture a minima en ville. Depuis la COP 21 la France a lancé la journée mondiale sans voiture, elle a lieu un dimanche de septembre. De nombreux métropoles du monde ont suivi. Objectif: apprendre à vivre la ville autrement pendant une journée et faire l’expérience qu’au quotidien on peut se déplacer différemment. Motivation supplémentaire: notre santé. En effet, selon une étude de l’insee, les admissions aux urgences pour affections aiguës et voies respiratoires augmentent significativement lorsque les transports en commun sont en grève et comprend donc davantage notre cher bagnole.

Pour aller plus loin, cet Atlas qui révèle grâce à plus de 100 cartes les changements qui bousculent l’ancien monde de l’automobile et donne les clés pour comprendre le nouveau. (Allez à la bibliothèque disponible sur ce site)

Voici une revue d’autres formules et une formulation mathématiquement exacte qui est valable sur toute la gamme des valeurs de Re.

C. T. GOUDAR,* Bayer HealthCare, Berkeley, Californie, et J. R. SONNAD,

Centre des sciences de la santé de l’Université de l’Oklahoma, Oklahoma City, Oklahoma

L’estimation du facteur de frottement est un élément clé de la conception d’un système de tuyauterie et l’équation de Colebrook-White est généralement la méthode de choix pour calculer le facteur de frottement d’un écoulement turbulent dans des conduites rugueuses :

Il relie implicitement le facteur de frottement f à la rugosité du tuyau, e/D, et au nombre de Reynolds : Re.
En raison de la nature implicite de l’Eq. I, les méthodes graphiques ont été proposées à l’origine pour l’estimation de f et sont encore utilisées aujourd’hui. Bien que la représentation visuelle dans une corrélation graphique soit certainement attrayante, la détermination précise de f est difficile et cette approche n’est pas adaptée à la plupart des projets de conception de systèmes de tuyauterie informatisés.

Pour la mise en œuvre informatique, des méthodes numériques itératives telles que la méthode Newton-Raphson peuvent être utilisées pour déterminer f à partir de l’équation 1.

Idéalement, ces calculs itératifs ne sont pas souhaitables, et dans une tentative de simplifier l’estimation de f à partir de l’Eq. I, plusieurs approximations explicites de f  ont été proposées. La précision des valeurs déterminées à partir de ces corrélations varie considérablement et toutes les corrélations ne sont pas valides sur une large plage Re (généralement 4 000 < Re < 108) pour être universellement applicables. La précision des corrélations empiriques non itératives a été évaluée de manière exhaustive et s’est avérée être comprise entre 1,42 et 28,23 % par rapport à une erreur de 1 % pour une forme simplifiée d’une représentation vraiment explicite de l’équation. 1.

En plus des corrélations non itératives mentionnées, plusieurs approximations itératives ont également été proposées pour l’Eq. 1

Il s’agit de relations fonctionnelles plus complexes entre f, e/D et Re, mais elles donnent des valeurs de f avec une plus grande précision. Pour éliminer complètement le besoin de corrélations empiriques, nous avons proposé une formulation explicite et mathématiquement exacte de l’équation 1 qui est valide sur toute la plage de valeurs Re et donne des valeurs f très précises. La précision d’une forme simplifiée de cette formulation a été présentée précédemment et dans cette étude, nous présentons une comparaison de deux autres formes de cette formulation avec les diverses approximations itératives de l’équation 1.

Pour éliminer complètement le besoin de corrélations empiriques, nous avons proposé une formulation explicite et mathématiquement exacte de l’équation. 1 qui est valable sur toute la plage des valeurs Re et donne des valeurs f très précises

Des détails sur la dérivation de la reformulation explicite ont été présentés ailleurs et seules les équations finales sont présentées ici. Le facteur de frottement f peut être explicitement lié à e/D et Re comme :

où:

Deux formulations différentes sont disponibles pour 8, la formulation linéaire, 8LA, et la formulation de fractions continues, 8cFA, et elles varient en complexité et en précision :

Ainsi, deux versions de l’équation 2 sont possibles selon le choix de 8 :

Une comparaison des propriétés de diverses approximations empiriques itératives de l’Eq. 1 est présenté avec l’erreur dans les estimations de f à partir des équations. 4 et 5.

Comparaison avec des approximations empiriques. La précision des Eqs. 4 et 5 et les approximations itératives empiriques de l’Eq. 1 ont été déterminés sur un espace rectangulaire de valeurs e/D et Re. Un ensemble de 20 valeurs e/D correspondant à celles utilisées par Moody a été sélectionné, couvrant une plage de 10-6 à 5 x 10-2. Pour chaque valeur e/D 500 valeurs de Re, réparties uniformément dans l’espace logarithmique sur 4 000 <Re< 108, ont été choisies. La précision des valeurs f à ces 10 000 points (grille de 20 x 500 de valeurs e/D et Re) a été déterminée en les comparant à celles obtenues à partir du formulaire mathématiquement équivalent très précis.

Un total de 10 000 valeurs f et leur erreur associée ont été déterminées sur la grille 20 x 500 des valeurs e/D et Re, et les valeurs d’erreur maximales sont indiquées dans le tableau 1. Bien que toutes les corrélations du tableau 1 ne soient pas valides sur l’ensemble de la plage Re (4 000 <Re< 108) , la comparaison a été faite intentionnellement sur cette plage étendue pour refléter les conditions de fonctionnement. L’erreur f maximale variait de 1,01 à 3,10 x 10-3 %, la corrélation de Serghides étant la plus précise. Les corrélations 8 et 9, qui sont dérivées d’une représentation mathématiquement équivalente explicite de l’équation 1, ont été caractérisées par des erreurs f maximales de 3,64 x 10-4 et 1,04 x 10-10 %, toutes deux meilleures que la meilleure approximation itérative disponible.

La précision des corrélations du tableau 1 est illustrée aux Fig. 1 et 2 où le pourcentage maximum d’erreur f est indiqué à différentes valeurs e/D. Pour chaque valeur e/D, 500 valeurs f ont été déterminées à 500 valeurs Re espacées de manière logarithmique dans la plage de 4 000 <Re< 108 et les valeurs maximales sont indiquées sur les Fig. 1 et 2. L’équation de Serghides (corrélation 7) avec une erreur maximale de 3,1 x 10-3 % est la meilleure approximation empirique disponible. La figure 3 montre une comparaison des profils d’erreur f pour l’équation de Serghides avec ceux des équations. 4 et 5. Erreur maximale d’Eqs. 4 et 5 étaient de 3,64 x 10-4 et 1,04 x 10-10 %, respectivement, et cette précision améliorée est reflétée dans la Fig. 3.

L’objet de cet article est de fournir à l’ingénieur un moyen simple d’estimer les facteurs de frottement à utiliser pour calculer la perte de charge dans des conduites neuves propres et dans des conduites fermées pleines à débit constant. Les développements modernes dans l’application de l’hydrodynamique théorique au problème du frottement des fluides sont impressionnants et dispersés dans une abondante littérature. Cet article ne se veut pas une étude critique de ce vaste domaine. Pour une revue concise, le petit livre du professeur Bakhine teff sur la mécanique de l’écoulement des fluides est une excellente référence. Prandtl et Tietjeris, et Rouse ont également apporté des contributions notables au sujet. L’auteur ne prétend pas offrir quoi que ce soit de particulièrement nouveau ou original, son but étant simplement d’incarner les conclusions désormais acceptées sous une forme pratique pour une utilisation technique. Dans la présente étude sur l’écoulement des canalisations, le facteur de frottement, désigné par f dans les graphiques ci-joints, est le coefficient de la formule de Darcy. dans lequel hf : la perte de charge en frottement, en pieds de colonne de fluide du fluide qui s’écoule ; L et D la longueur et le diamètre interne du tuyau en pieds ; V : la vitesse moyenne d’écoulement en pieds par seconde ; g : l’accélération de la gravité en pieds par seconde par seconde. Le facteur f est une quantité sans dimension, et aux vitesses ordinaires est une fonction de deux, et seulement deux, autres quantités sans dimension : la rugosité relative de la surface, e/D (e étant une quantité linéaire en pieds représentative de la rugosité absolue) , et le nombre de Reynolds R = VD / v (v étant le coefficient de viscosité cinématique du fluide en pieds carrés par seconde). La figure 1 donne les valeurs numériques de f en fonction de e/D et R. Il y a dix ans, R. J. S. Pigott (4) a publié un tableau pour le même facteur de frottement, en utilisant les mêmes coordonnées que sur la figure 1 de cet article. Son tableau s’est avéré très utile et pratique et a été reproduit dans un certain nombre de textes (5). Le tableau de Pigott était basé sur une analyse de quelque 10 000 expériences provenant de diverses sources (6), mais n’avait pas l’avantage, pour tracer ou ajuster les courbes, des développements ultérieurs dans les formes fonctionnelles des courbes. La même année, Nilruradse (7) publie ses expériences sur des tuyaux artificiellement rugueux. Sur la base des tests de Nikuradse et d’autres, von Karman (8) et Prandtl (9) ont développé leurs analyses théoriques de l’écoulement des tuyaux et nous ont donné des formules appropriées avec des constantes numériques pour le cas de tuyaux parfaitement lisses ou ceux dans lesquels les irrégularités sont petites par rapport à l’épaisseur de la couche limite laminaire, et pour le cas des conduites rugueuses où les rugosités dépassent suffisamment pour briser la couche laminaire, et l’écoulement devient complètement turbulent. L’analyse n’a cependant pas couvert l’ensemble du champ mais a laissé un vide, à savoir ; la zone de transition entre les tuyaux lisses et rugueux, la région de turbulence incomplète. Les tentatives pour combler cette lacune par l’utilisation des résultats de Nikuradse pour la rugosité artificielle produite par des grains de sable serrés, n’étaient pas adéquates, puisque les résultats étaient clairement différents de l’expérience réelle pour les surfaces ordinaires rencontrées dans la pratique. Les courbes de Nikuradse ont montré une forte baisse suivie d’une courbe inverse particulière non observée avec les surfaces commerciales, et nulle part suggérée par le graphique de Pigott basé sur de nombreux tests. Récemment Colebrook (11), en collaboration avec C. M. White ; a développé une fonction qui donne une forme pratique de courbe de transition pour combler l’écart. Cette fonction s’accorde avec les deux extrêmes de rugosité et donne des valeurs en accord très satisfaisant avec les mesures réelles sur la plupart des formes de tuyauterie commerciale et des surfaces de tuyauterie habituelles. Rouse (12) a montré qu’il s’agissait d’une solution raisonnable et pratiquement adéquate et a tracé un tableau basé sur celle-ci. Afin de simplifier le tracé, Rouse a adopté des coordonnées peu pratiques pour une utilisation ordinaire en ingénierie puisque f est implicite dans les deux coordonnées et que les valeurs R sont représentées par des coordonnées courbes, de sorte que l’interpolation pose certains problèmes

L’auteur a dressé une nouvelle carte, Fig. 1, sous la forme plus conventionnelle utilisée par Pigott, en profitant des relations fonctionnelles établies ces dernières années. Les courbes de f par rapport à R sont tracées à des échelles logarithmiques pour diverses valeurs constantes de rugosité relative e/D et pour permettre une sélection facile de e/D, un tableau d’accompagnement, Fig. 2, est donné à partir duquel i peut être lu pour n’importe quelle taille de tuyau d’un type de surface donné.

Pour trouver la perte par frottement d’un tuyau, la procédure est la suivante :
Trouvez le e/D approprié à partir de la Fig. 2, puis suivez la ligne correspondante, ainsi identifiée, sur la Fig. 1, à la valeur du nombre de Reynolds R correspondant à la vitesse d’écoulement. Le facteur f est ainsi trouvé, à utiliser dans la formule de Darcy

Sur la figure 2, les échelles en haut et en bas donnent les valeurs du diamètre en pieds et en pouces. La figure 1 n’implique que des grandeurs sans dimension et est applicable dans n’importe quel système d’unités.

Pour faciliter le calcul de R, des échelles auxiliaires sont indiquées en haut de la Fig. 1, donnant les valeurs du produit (VD ») pour deux fluides, c’est-à-dire l’eau et l’air atmosphérique, à 60 F. (D » est le diamètre intérieur en pouces.) Comme autre auxiliaire,. La figure 3 est donnée, à partir de laquelle R peut être rapidement trouvé pour l’eau à des températures ordinaires, pour n’importe quelle taille de tuyau et vitesse moyenne V. Des lignes pointillées sur ce graphique ont été ajoutées pour donner les valeurs du débit ou de la quantité de fluide qui s’écoule, Q = AV, exprimé à la fois en pieds cubes par seconde et en gallons américains par minute.

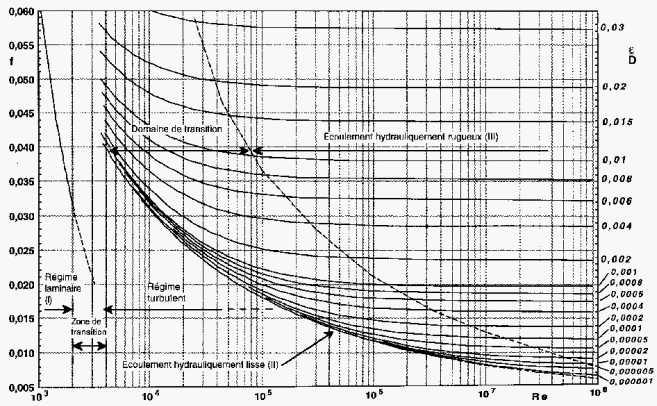
Comparison- of the iterative approximations of the Colebrook-White equation

Here’s a review of other formulas and a mathematically exact formulation that is valid over the entire range of Re values

C. T. GOUDAR,* Bayer HealthCare, Berkeley, California, and J. R. SONNAD,

University of Oklahoma Health Sciences Center, Oklahoma City, Oklahoma

Friction factor estimation is a key component of piping sys­tem design and the Colebrook-White equation is typically the method of choice for computing turbulent flow friction factor in rough pipes:

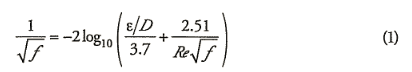
It relates the friction factor f implicitly to the pipe roughness, elD, and the Reynolds number, Re. Because of the implicit nature of Eq. I, graphical methods were originally proposed for f estima­tion¹ and are still used today. While the visual representation in a graphical correlation is certainly appealing, accurate f determina­tion is difficult and this approach is not suited for most current computer-based piping system design projects.

For computer implementation, iterative numerical methods such as the  Newton-Raphson method² can be used to  determine f from Eq. 1. Ideally, these iterative calculations are not desirable, and in an attempt to simplify f estimation from Eq. I, several explicit approximations of f  have been proposed.^3-6 Accuracy of values determined from these correlations varies greatly and not all correlations are valid over a large Re range (typically 4,000 < Re < 10⁸) to be universally applicable. Accuracy of the noniterative empirical correlations has been comprehensively evaluated7 and was found to be in the 1.42-28.23% range compared with 1% error for a simplifled form of a truly explicit representation of Eq. 1.

In addition to the noniterative correlations mentioned, several iterative approximations have also been proposed for Eq. 1_4- , 6 , 8  9

These are more complex functional relationships between f, e/D and Re but result in f values with higher accuracy. To completely eliminate need for empirical correlations, we have proposed an explicit, mathematically exact formulation of Eq. 1 that is valid over the entire range of Re values and results in highly accurate f values. ^{10, 11} Accuracy of a simplifled form of this formulation was presented earlier⁷ and in this study we present a comparison of two other forms of this formulation with the various iterative approximations of Eq. 1.

To completely eliminate need for empirical correlations, we have proposed an explicit, mathematically exact formulation of Eq. 1 that is valid over the entire range of Re values and results in highly accurate f values

Details on the derivation of the explicit reformulation have been presented elsewhere¹¹ and only the final equations are shown here. The friction factor f can be explicitly related to e/D and Re as:

where:

Two different formulations are available for 8, the linear for­mulation, 8LA, and the continued fractions formulation, 8cFA and they vary in complexity and accuracy:

Thus, two versions of Eq. 2 are possible depending upon the choice of 8:

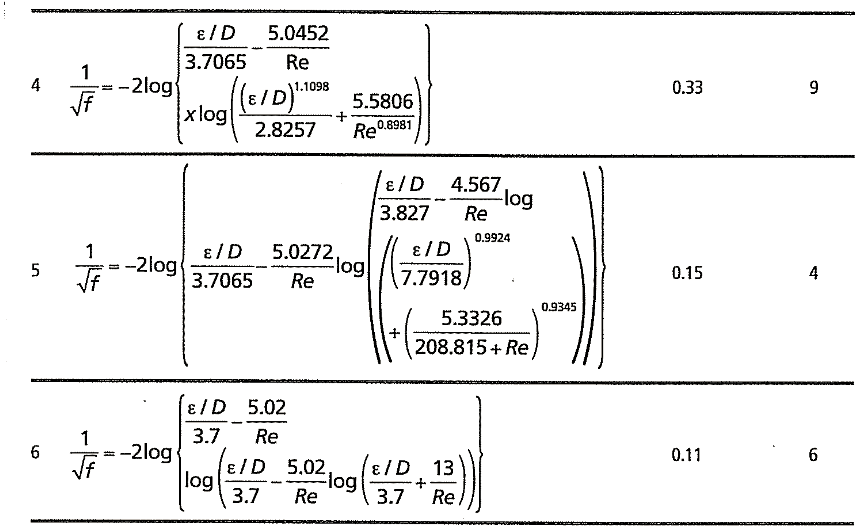
A comparison of the properties of various iterative empirical approximations of Eq. 1 is presented along with error in f’ estimates from Eqs. 4 and 5.

Comparison with empirical approximations. The accuracy of Eqs. 4 and 5 and the empirical iterative approxima­tions of Eq. 1 were determined over a rectangular space of e/D and Re values. A set of 20 e/D values corresponding to those used by Moody¹ were selected that spanned a range from 10^-6 to   5 x 10^-2. For each e/D value 500 values of Re, distributed uniformly in the logarithmic space over 4,000 <Re< 10⁸, were chosen. Accuracy of f  values at these 10,000 points (20 x 500 grid of e/D and Re values) was determined by comparing them with those obtained from the highly accurate mathematically equivalent form.¹¹

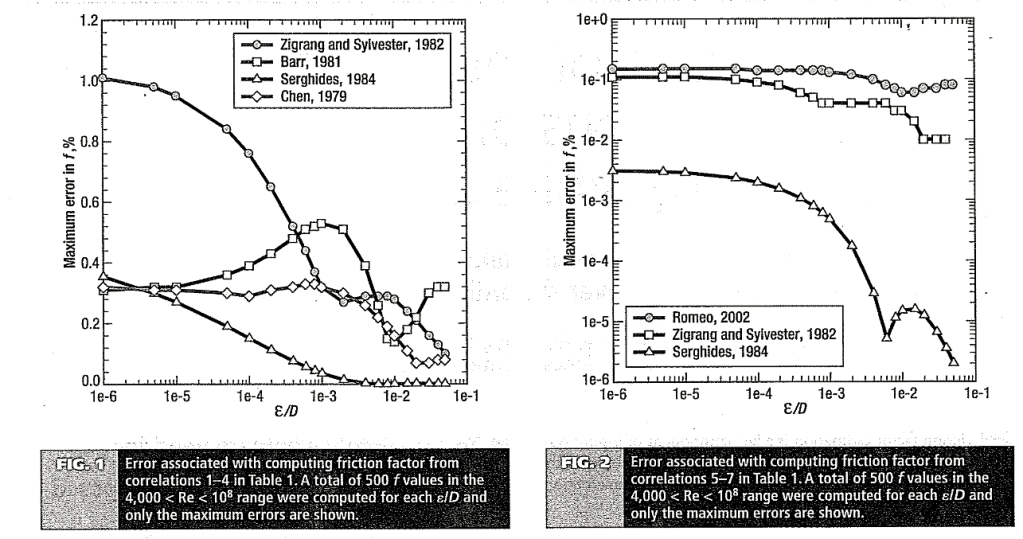
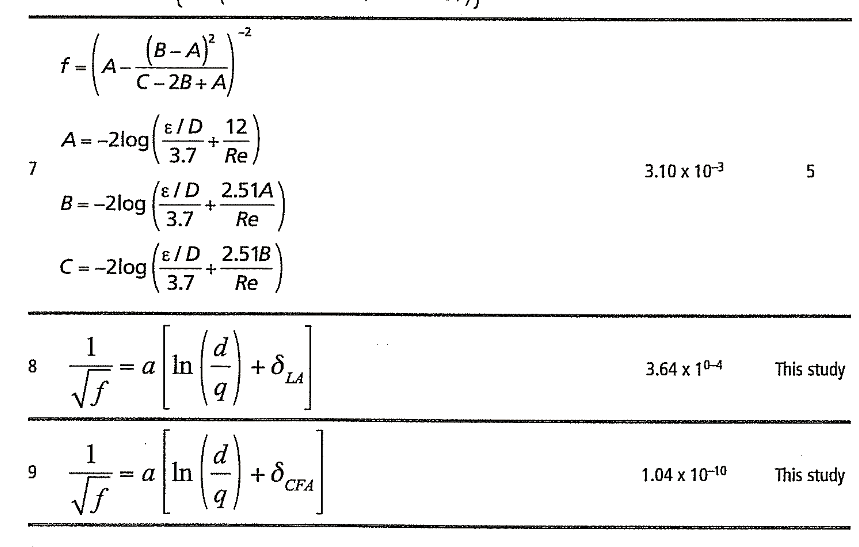
A total of 10,000 f values and their associated error were determined over the 20 x 500 grid of e/D and Re values, and the maximum error values are shown in Table 1. While not all Table 1 correlations are valid over the entire Re range (4,000 <Re< 10⁸⁾ , comparison was intentionally made over this extended range to reflect operational conditions. The maximum f error ranged from 1.01 to 3.10 x 10^-3% with the Serghides correla­tion5 being the most accurate. Correlations 8 and 9, which are derived from an explicit mathematically equivalent representation of Eq. 1, were characterized by maximum f  errors of 3.64 x 10^-4 and 1.04 x 10^{– 10} %, both better than the best available iterative approximation.

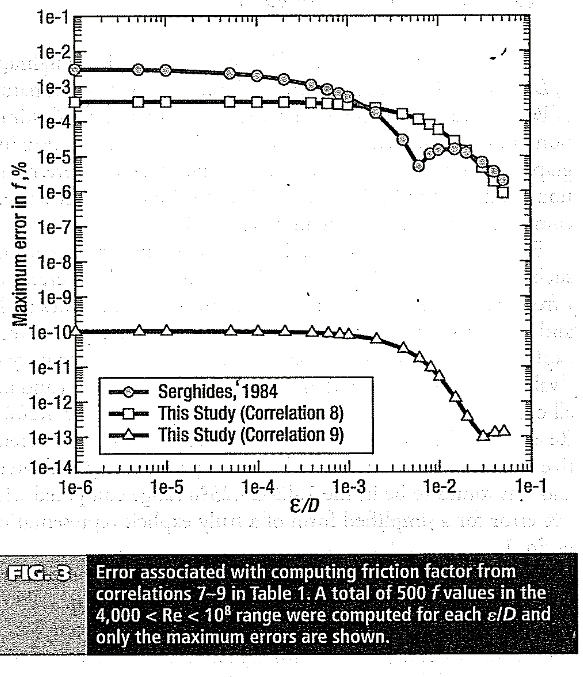
Accuracy of the correlations in Table 1 is shown in Figs. 1 and 2 where the maximum percentage f error is shown at varying e/D values. For each e/D value, 500 f values were determined at 500 logarithmically spaced Re values in the 4,000 <Re< 10⁸ range and the maxi­mum values are shown in Figs. 1 and 2. The Serghides equation (correlation 7) with a maximum  error of 3.1 x  10^-3% is the best available empirical approxi­mation. Fig. 3 shows a comparison of f error profiles for the Serghides equation with those from Eqs. 4 and 5. Maximum error from Eqs. 4 and 5 were 3.64 x10^-4 and 1.04 x 10^{– 10}%, respectively, and this improved accuracy is reflected in Fig. 3.

LITERATURE CITED

1 Moody, L. F. « Friction factors for pipe flow, » Trans. ASME 66, 1944, pp. 671-684.

2 Press, W. H., et al., Numerical Recipes in FORTRAN: The an of scientific computing, New York Cambridge University Press, 1992.

3 Gregory, G. A. and M. Fogarasi, « Alternate to standard friction factor equation, » Oil and Gas Journal 1985, pp. 120-127.

4 Romeo, E., C. Royo, and A. Monzon, « Improved explicit equations for estimation of the friction factor in rough and smooth pipes, » Chem Eng. 86, 2002, pp. 369-374.

5 Serghidcs, T. K, « Estimate friction factor accu-rately, » Chem. Eng. 91, 1984, pp. 63-64.

6 Zigrang, D. J., and N. D. Sylvester, « Explicit approximations to the solution of Colebrook’s friction faaor equation, » AIChE J. 28, 1982, pp. 514-515.

7 Goudar, C. T. and J. R. Sonnad, « Explicit friction factor correlation for turbulent flow in rough pipe, » Hydrocarbon Processing 86, 2007, pp. 103-105.

8 Barr, D. I. H.; « Solutions of the Colebrook-White function for resistance to uniform turbulent flow, » Proc. Inst. Civil big. 71, 1981, pp. 529-535.

9 Chen, N. H., « An explicit equation for friction factor in pipe, » Ind Eng. Chem. Fund. 18, 1979, pp. 296-297.

10 Sonnad, J. IL and C. T. Goudar, « Turbulent flow friction factor calculation using a mathematically-exact alternative to the Colebrook-White equation, J. Hydr. Eng. 132, 2006, pp. 863-867.

11 Sonnad, J. R. and C. T. Goudar, « Explicit reformulation of the Colebrook-White equation for turbulent flow friction factor calculation, » Intl Eng. Chem. Res. 46, 2007, pp, 2593-2600.

Friction Factors for Pipe Flow

Br LEWIS F. MOODY,’ PRINCETON, N. J.

The object of this paper is to furnish the engineer with a simple means of estimating the friction factors to be used in computing the loss of head in clean new pipes and in closed conduits running full with steady flow. The modern developments in the application of theoretical hydrodynamics to the fluid-friction problem are impressive, and e scattered through an extensive literature. This paper is not intended as a critical survey of this wide field. .For a concise review, Professor Bakhmeteff’s (1)2 small book on the mechanics of fluid flow is an excellent reference. Prandtl and Tietjens (2) and Rouse (3) have also made notable contributions to the subject. The author does not claim to offer anything particularly new or original, his aim merely being to embody the now accepted conclusions in convenient form for engineering use.

In the present pipe-flow study, the friction factor, denoted by f in the accompanying charts, is the coefficient in the Darcy formula

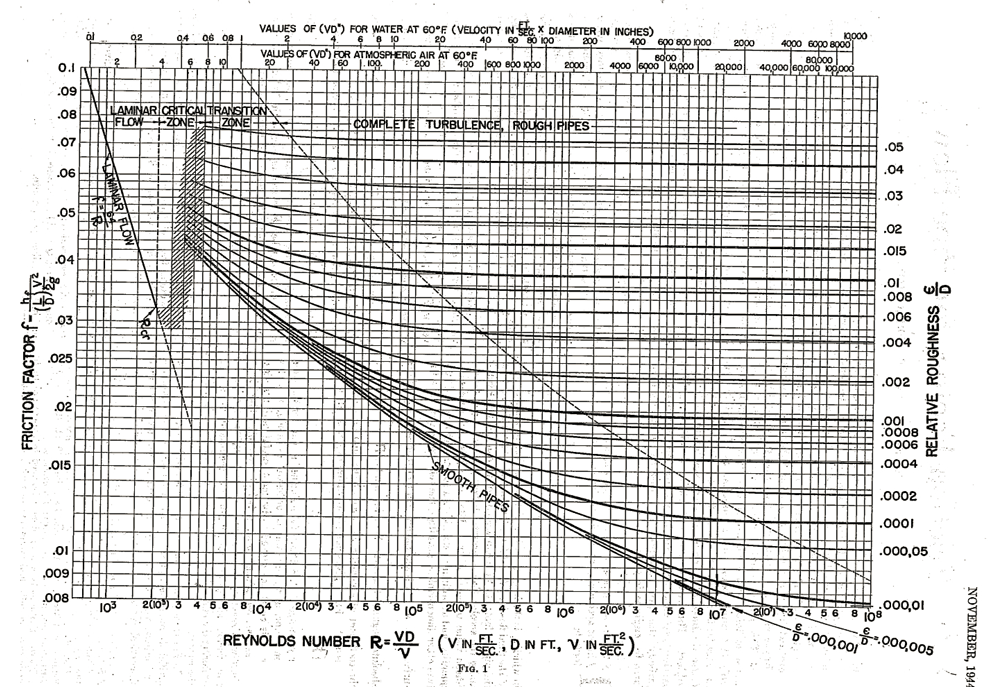
in which h_f is the loss of head in friction, in feet of fluid column of the fluid flowing; L and D the length and internal diameter of the pipe-in.-feet; V the mean velocity of flow in feet per second; and g the acceleration of gravity in feet per second per second (mean Value taken as 32.16). The factor f is a dimensionless quantity, and at ordinary velocities is a function of two, and only two, other dimensionless quantities, the relative roughness of the surface, e/D (e being a linear quantity in feet representative of the absolute roughness), and the Reynolds number R = VD /v (v being the coefficient of kinematic viscosity of the fluid in square feet per second). Fig. 1 gives numerical values of f as a function of e/D and R.

Ten years ago R. J. S. Pigott (4) published a chart for the same friction factor, using the same co-ordinates as in ‘Fig. 1 of this paper. His chart has proved to be most useful and practical and has been reproduced in a number of texts (5). The Pigott chart was based upon an analysis of some 10,000 experiments from various sources (6), but did not have the benefit, in plotting or fairing the curves, of later developments in functional forms of the curves.

In the same year Nikuradse (7) published his experiments on artificially roughened pipes. Based upon the tests of Nikuradse and others, von Karman (8) and Prandtl (9) developed their theoretical analyses of pipe flow and gave us suitable formulas with numerical constants for the case of perfectly smooth pipes or those in which the irregularities are small compared to the thickness of the laminar boundary layer, and for the case of rough pipes where the roughnesses protrude sufficiently to break up the laminar layer, and the flow becomes completely turbulen

^{i Professor, Hydraulic Engineering, Princeton University. Mem. A.S.M.E.}

^{2 Numbers in parentheses refer to the Bibliography at the end of the paper}.

^{Contributed by the Hydraulic Division and presented at the Semi-Annual Meeting, Pittsburgh, Pa., June 19-22, 1944, of THE}

^{MEIBRICAN SOCIETY OF MECHANICAL ENGINEERS}

^{Nom: Statements and opinions advanced in papers are to be understood as individual expressions of their authors and not those of the Society.}

The analysis did not, however, cover the entire field but left a gap, namely; the transition zone between smooth and rough pipes, the region of incomplete turbulence. Attempts to fill this gap by the use of Nikuradse’s results for artificial roughness produced by closely packed sand grains, were not adequate, since the results were clearly at variance from actual experience for ordinary surfaces encountered in practice. Nikuradse’s curves showed a sharp drop followed by a peculiar reverse curve, not observed with commercial surfaces, and nowhere suggested by the Pigott chart based on many tests.

Recently Colebrook (11), in collaboration with C. M. White; developed a function which gives a practical form of transition curve to bridge the gap. This function agrees with the two extremes of roughness and gives values in very satisfactory agreement with actual measurements on most forms of commercial piping and usual pipe surfaces. Rouse (12) has shown that it is a reasonable and practically adequate solution and has plotted a chart based upon it. In order to simplify the plotting, Rouse adopted co-ordinates inconvenient for ordinary engineering use, since f is implicit in both co-ordinates, and R values are represented by curved co-ordinates, so that interpolation is troublesome.

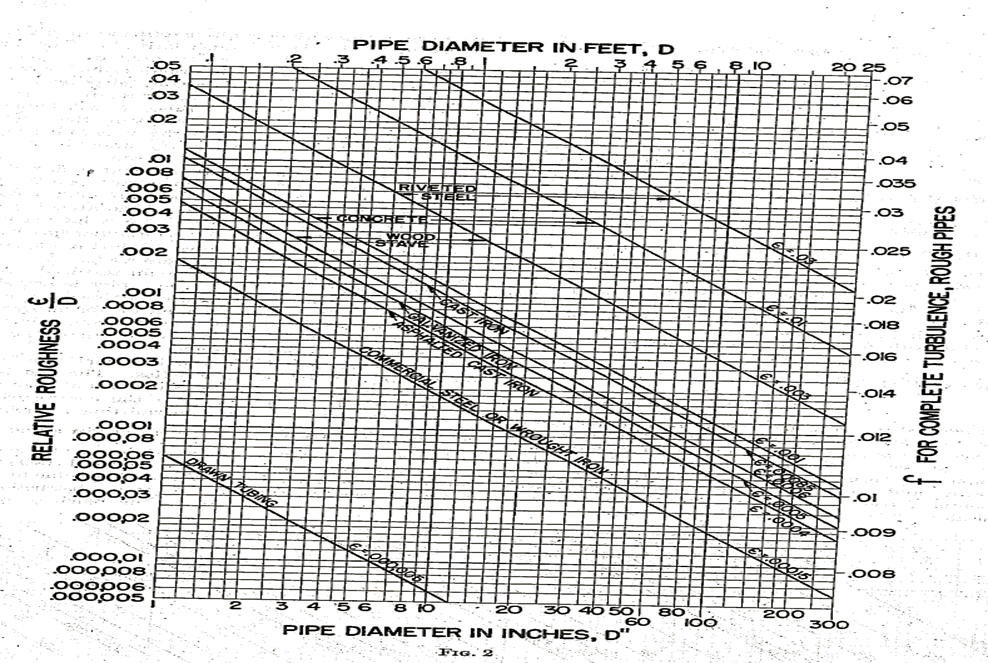
The author has drawn up a new chart, Fig. 1, in the more conventional form used by Pigott, taking advantage of the functional relationships established in recent years. Curves of f versus R are plotted to logarithmic scales for various constant values of relative roughness (e/D); and to permit easy selection of e/D, an accompanying chart, Fig. 2, is given from which e/D can be read for any size of pipe of a given type of surface.

In order to find the friction loss in a pipe, the procedure is as follows: Find the appropriate (e/D) from Fig. 2, then follow the corresponding line, thus identified, in Fig. 1, to the value of the Reynolds number R corresponding to the velocity of flow. The factor f is thus found, for use in the Darcy formula

In Fig. 2, the scales at the top and bottom give values of the diameter in both feet and inches. Fig. 1 involves only dimensionless quantities and is applicable in any system of units.

To facilitate the calculation of R, auxiliary scales are shown at the top of Fig. 1, giving values of the product (V.D ») for two fluids, i.e., water and atmospheric air, at 60 F. (D » is the inside diameter in inches.) As a further auxiliary, Fig.3 is given, from Which R can be quickly found for water at ordinary temperatures, for any size of pipe and mean velocity V. Dashed lines on this chart have been added giving values of the discharge or quantity of fluid flowing, Q = AV, expressed in both -cubic feet per second and in U. S. gallons per minute.

^{3 Rouse, reference (3), p. 250; and Powell, reference (10), p. 174.}

For other fluids, the kinematic viscosity v may be found from Fig. 4, which with. Prof. R. L. Daugherty’s kind permission has been reproduced to enable R to be quickly found for various fluids, Fig. 4 includes an auxiliary diagram constructed by Dr. G. F. Wislicenus, which gives R for various values of the product VD » shown by the diagonal lines. – For any value of v in the left-hand diagram, by following a horizontal line to the appropriate diagonal at the right, the corresponding R may be read at the top of the auxiliary graph.

Over a large part of Fig. 1, an approximate figure for R is sufficient, since f varies only slowly with changes in R; and in the rough-pipe zone f is independent of R. From the last consideration, it becomes possible to show, in the right-hand margin of Fig. 2, values of f for rough pipes and complete turbulence.

^{Reference (13) and reference (5).}

If it is seen that the conditions of any problem clearly fall in the zone of complete turbulence above and to the right of the dashed line in Fig. 1, then Fig. 2 will give the value of f directly without further reference to the other charts.

ILLUSTRATION OF USE OF CHARTS

Example 1: To estimate the loss of head in 200 ft of 6-in. asphalted cast-iron pipe carrying water with a mean velocity of 6 fps: In Fig. 2, for 6 in. diam (bottom. scale), the diagonal for « asphalted cast iron » gives e/D= 0.0008 (left-hand margin). In Fig. 3, for 6 in. diam (left-hand margin), the diagonal for V = 6 fps gives R = 2.5 (10⁵) (bottom scale) (or, instead of using Fig. 3, compute VD » = 6 _X 6 = 36). In Fig. 1, locate from the right-hand margin the curve for e/D= 0.0008 and follow this curve to a point above R = 2.5 (10⁵) on the bottom scale (or below VD » = 36 on the top scale). This point gives f = 0.02 (left-hand margin); then:

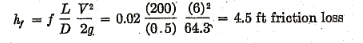
Example 2: To estimate the loss of head per 100 ft in a 15-in. new cast-iron pipe, carrying water with a mean velocity of 20 fps: In Fig. 2, for 15 in. dim (bottom scale), the diagonal for « cast iron » gives e/D= 0.0007 (left-hand margin). In Fig. 3, for 15 in. diam (left-hand margin), the diagonal for V = 20 fps gives R = 2 (10⁶) (or, instead of using Fig. 3, compute VD »= 20 X 15= 300). In Fig. 1, the curve for e/D= 0.0007 (interpolating between 0.0006 and 0.0008, right-hand margin), at a point above R = 2 (10⁶) (bottom scale) (or below VD » = 300, top scale) gives f = 0.018 (left-hand margin). In this case the point on Fig. 1 falls just on the boundary of the region of « complete turbulence; rough pipes. » Here R or VD » need only be approximated sufficiently to see that the point falls in the complete turbulence region, and f can then be found directly from the right-hand margin in Fig. 2 without further reference to Fig. 1; then

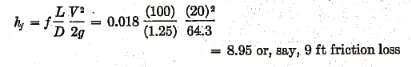
It must be recognized that any high degree of accuracy in determining f is not to be expected. With smooth tubing, it is true, good degrees of accuracy are obtainable; a probable variation in f within about ±5 per cent (14), and for commercial steel and wrought-iron piping, a variation within about ±10 per cent. But, in the transition and rough-pipe regions, we lack the primary and obvious essential, a technique for measuring the roughness of a pipe mechanically. Until such a technique is developed, we have to get along with descriptive terms to specify the roughness; and naturally this leaves much latitude. The lines in Fig. 2 might be more graphically represented by broad bands rather than single lines, but this is not practical due to overlapping.

Even with this handicap, however, fairly reasonable estimates of friction loss can be made, and, fortunately, engineering problems rarely require more than this. It will be noted from the charts that a wide variation in estimating the roughness affects f to a much smaller degree. In the rough-pipe region, for the reasons just explained, the values of f cannot be relied upon within a range of the order of at least 10 per cent.

The charts apply only to new and clean piping, since the rapidity of deterioration with age, dependent upon the quality of the water or fluid and that of the pipe material, can only be guessed in most cases; and in addition to the variation in roughness there may be, in old piping, an appreciable reduction in effective diameter, making an estimate of performance speculative.

Although we have no accepted method of direct measurement of the roughness, in any case where we have a sample of pipe of the same surface texture available for test in the laboratory or in the field, then from a test of such a pipe in any size we can, by aid of the charts, find the absolute roughness corresponding to its performance. Thus we have a means for measuring the Toughness hydraulically. The scale of the absolute roughness e used in plotting the charts is arbitrary, based upon the sand-grain diameters of Nikuradse’s experiments.

The field covered by Fig. 1 divides itself into four areas representing distinct flow characteristics. The first is the region of laminar flow, up to the critical Reynolds number of 2000. Here the flow is fully stabilized under the control of viscous forces which damp out turbulence, permitting a completely rational solution. The values off are here given by a single curve, f = 64/R independent of roughness, representing the Hagen -Poiseuille law.

Between Reynolds numbers of 2000 and 3000 or 4000, the conditions depend upon the initial turbulence due to such extraneous factors as sudden changes in section, obstructions, or a sharp-edged entrance corner prior to the reach of pipe considered;

and the conditions are probably also affected by pressure waves initiating instability. This region has been called a critical zone, and the indefiniteness of behavior in this region has been indicated by a hatched area without definite f lines. The minimum for f values is the dotted continuation of the laminar-flow line, corresponding to very smooth and steady initial flow. When there is distinct turbulence in the entering fluid, the flow in the’ critical zone is likely to be pulsating (2) rather than steady. The effects of strong initial turbulence may even extend into the laminar-flow zone, raising the f values somewhat, as far as to a Reynolds number of about 1200. Above a Reynolds number of 3000 or 4000, conditions again become reasonably determinate. Here we find two regions, namely, the transition zone and the rough-pipe zone. The transition zone extends upward from the line for perfectly smooth pipes, for which the equation is

                                                                                             (Karman., Prandtl, Nikuradse)  to the dashed line indicating its upper limit, plotted

from the relation

                                           (following the corresponding line in Rouse’s chart, reference 12).

In the transition zone the curves follow the Colebrook function.

These curves are asymptotic at one end to the smooth pipe line and at the other to the horizontal lines of the rough-pipe zone. Actually, the curves converge rapidly to these limits, merging with the smooth pipe line at the left, and at the right, beyond the dashed line, becoming indistinguishable from the constant f lines for rough pipe.

THE COLEBROOK FUNCTION

The basis of the Colebrook function may be briefly outlined. Von Kerman had shown that, for completely turbulent flow in rough pipes, the expression

is equal to a constant (1.74), or, as expressed by Colebrook,  

is equal to-zero. In the transition region of incomplete turbulence von Karman’s expression is not equal to a constant but to some function of the ratio of the size of the roughnesses to the thickness of the laminar boundary layer. Accordingly, Nikuradse had represented his experimental results on artificially roughened pipes by plotting

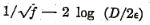
                                      versus

in which   

is the laminar layer thickness. By this method of plotting, the results for all types of flow and degrees of roughness were shown to fall on a single curve. Using logarithmic scales, the smooth-pipe curve becomes an inclined straight line, and the rough-pipe curves merge in a single horizontal line.

Colebrook (11), using equivalent co-ordinates,⁵ plotted in his Fig. 1, here reproduced as Fig. 5, the results of many groups of tests on various types of commercial pipe surfaces. He found that each class of commercial pipe gave a curve of the same form, and while these curves are quite different from Nikuradse’s sand-grain results, they agree closely with each other and with a curve representing his transition function.

^{t’e/a may be expressed in alternative forms as proportional to R-Vf in which r = D/2, k = e; or to p V*k in which V* = ‘ r/k  ‘2 . Ti’ To being the shearing stress at the pipe wall, p the mass density of the fluid andµ its absolute or dynamic viscosity.}

Rouse « (12), also using equivalent co-ordinates, has plotted in his Fig. 6, here reproduced as Fig. 6, a large number of points each of which represents a series of tests on a given size of commercial pipe, together with the Colebrook curve. As he points out, the deviation of the points from the Colebrook curve « is evidently not much greater than the experimental scatter of the individual measurements in any one series ».

When the thickness of the laminar layer, which decreases with increasing Reynolds number, becomes so small, compared to the surface irregularities, that the laminar flow is broken up into turbulence, the flow conditions pass over into the zone of « rough pipes, » with complete turbulence established practically throughout the flow. Viscous forces then become negligible compared to inertia forces, and f ceases to be a function of the Reynolds number and depends only upon the relative roughness; giving horizontal lines of constant f in the chart. These lines agree with the von Karman rough-pipe formula:

Since f depends upon the relative roughness, the ratio of the absolute roughness to the pipe diameter, even a fairly rough surface in a very large pipe gives a small relative roughness. Thus Colebrook plots the results obtained on the penstocks of the Ontario Power Company, where metal forms and specially laid concrete produced a very smooth example of concrete surface. This in combination with the large diameter gave a relative roughness comparable to drawn brass tubing, with f values falling practically on the « smooth pipe » line of Fig. 1. Such specially fabricated, welded-steel pipe lines as those of the Colorado aqueduct system would probably give values along the same curve.

On the other hand, at very high velocities in drawn tubing of small diameter, even the small absolute roughness is sufficient to break up the laminar boundary layer, and the tubing becomes in effect a « rough pipe. » Very few experiments have carried the velocities and Reynolds numbers high enough to permit a close estimate of e for drawn brass, copper, or similar tubing; but by applying the Colebrook function to the available data (14, 15), for the smoothest surfaces reported upon, e was estimated as of the order of 0.000005; and a line corresponding to this value has been drawn in Fig. 2, serving as a minimum limit for surfaces likely to be encountered in practice.

PIPE FRICTION FACTORS APPLIED TO OPEN-CHANNEL FLOW

Pipe friction factors have sometimes been applied to open-channel flow, and more commonly the friction losses in large pipes and other closed conduits have been computed from open-channel formulas. The Chezy formula for open channels is

in which V is the mean velocity; m the hydraulic mean depth or « hydraulic radius, » the sectional area divided by the wetted perimeter; S the slope, the loss of head divided by length of channel, and C a coefficient. The Chezy formula is equivalent to the Darcy formula for pipes, the Chezy coefficient C being convertible into f by the relation f= 8g/C². It should be considered, however, that the Chezy coefficients have been derived principally from observations on relatively wide and shallow channels of large area and rough bottoms, far from circular in shape, and that they involve a free water surface not present in closed conduits, so that; even when the flow is uniform, the problem is highly complex. Consequently, such formulas as Manning’s are recommended for open channels in preference to the use of values of C derived from the pipe friction factors.

Open channels dealt with in engineering practice are usually rough surfaced and of large cross section, corresponding to large Reynolds numbers and falling in the zone of complete turbulence, so that the friction factors are practically independent of Reynolds number. The presence of a free surface, however, with surface waves or disturbances, introduces a consideration not involved in closed-conduit flow. It is therefore the author’s view that while, for open channels, we can drop the Reynolds number as an index of performance, we should replace it by a new criterion, the Froude number relating the velocity head and depth, which can be expressed as

or more strictly               

                         

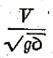
in which

denotes the average depth or, sectional area divided by the surface breadth; the latter form representing the .ratio of mean velocity to the gravitational critical velocity or velocity of propagation of surface waves.

This proposed criterion defines whether the flow falls in the « tranquil, » « shooting, » or critical state. The neglect of this factor may at least partially account for inconsistencies between various open-channel formulas, and between open-channel and pipe-friction formulas, and casts particular doubt on accepted formulas for open-channel friction in the critical or shooting-flow regions, These considerations suggest the plotting of open-channel friction factors as a function of the relative roughness and the Froude number, in similar manner to the plotting off as a function of the relative roughness and the Reynolds number for closed conduits.

For the foregoing reasons, Fig. 1 is not recommended with much confidence for general application to open channels, for which a formula such as Manning’s better represents the available information. The charts can however be applied, at least as an approximation, to noncircular closed conduits of not too eccentric a form or not too different from a circular section, by using an equivalent diameter

Since civil engineers usually classify surface roughness by the Kutter and Manning roughness factor n, it would be helpful in selecting a value of e for such variable surfaces as concrete, if we could correlate e and n. P. Panagos⁶ has applied the Colebrook function to the test data collected by Scobey (16) and finds the following values of e corresponding to the Rutter n ratings given by Scobey, which may be at least tentatively utilized:

Kutter n         0.0105   0.011      0.012   0.013   0.014   0.015  0.016

Absolute roughness e  0.00015    0.0005   0.002   0.005   0.011   0.02    0.03

Accordingly, on the basis of Scobey’s data the lines given in Fig. 2 for concrete may be somewhat more definitely described as follows:

Although the curves in Fig. 1 are plotted from definite functional forms which can be accepted with some confidence within the degree of accuracy required in engineering use, further information will be welcomed which would improve the location and definition of the lines in Fig. 2, or which would add new lines for other materials. Any tests of friction head in pipe of any material can be applied to Fig, 1, and corresponding points can be readily located in Fig. 2. A 45-deg line through a point so located can then be added to Fig. 2, to represent a particular kind of pipe surface.

ACKNOWLEDGMENT

For helpful suggestions and assistance, the author is particularly indebted to Prof. B. A. Bakhmeteff, Mr. Ralph Watson, Dr. G. F. Wislicenus, Dr, A. T. Ippen; and to Mr. P. Panagos for collecting data and numerical checking.

BIBLIOGRAPHY

1 « The Mechanics of Turbulent Flow, »-by B. A. Bakhmeteff, Princeton University Press, 1936.

2 « Applied Hydro- and Aeromechanics, » by L. Prandtl and 0. G. Tietjens, Engineering Societies MOnographs, McGraw-Hill Book Company, Inc., New York, N. Y., 1934.

3 « Fluid Mechanics for Hydraulic Engineers, » by H. Rouse, Engineering Societies Monographs, McGraw-Hill Book. Company, Inc., New York, N. Y., 1938.

4 « The Flow of Fluids in Closed Conduits, » by R. J. S. Pigott, Mechanical Engineering, vol. 55, 1933, pp. 497-501, 515.

5 « Hydraulics, » by R. L. Daugherty, McGraw-Hill Book Company, Inc., New York, N. Y., 1937.

6 « A Study of the Data on the Flow of Fluid in-Pipes, » by E. Keinler, Trans. A.S.M.E., vol. 55, 1933, paper Hyd-55-2, pp. 7-32.

7 « Stromungsgesetze in Rauhen Rohren, » by J. Nikuradse, V.D.Z.Forsch,ungsheft 361, Berlin, 1933, pp. 1-22.

8 « Mechanische Ihnlichkeit and Turbulenz, » by Th. von ICArman, Nachrichten von der Gesellschaft der Wissenschaften Fu Gottingen, 1930, Fachgruppe 1, Mathematik, no. 5, pp. 58-76. (« Mechanical Similitude and Turbulence, » Tech. Mem. NA.C.A.., no. 611, 1931.)

9 « Neuere Ergebnisse der Turbulenzforschung, » by L. Prandtl, Zeitschrift des Vereines deutscher Ingenieure, vol. 77, 1933, pp. 105-114.

10 « Mechanics of Liquids, » by R. W. Powell, the MacMillan Company, New York, N. Y., 1940.

11 « Turbulent Flow in Pipes, With Particular Reference to the Transition Region Between the Smooth and Rough Pipe Laws, » by C. F. Colebrook, Journal of the Institution of Civil Engineers (London, England), vol. 11, 1938-1939, pp. 133-156.

12 « Evaluation of Boundary Roughness, » by H. Rouse, Proceedings Second Hydraulic Conference, University of Iowa Bulletin 27, 1943.

13 « Some Physical Properties of Water and Other Fluids, » by R. L. Daugherty, Trans. A.S.M.E., vol. 57, 1935, pp. 193-196..

14 « The Friction Factors for Clean Round Pipes, » by T. B. Drew, E. C. Soo, and W. H. McAdams, Trans. American Institute of Chemical Engineers, vol. 28, 1932, pp. 56-72.

15 « Experiments Upon. the Flow of Water in Pipes and Pipe Fittings, » by J. R. Freeman, published by THE AMERICAN SOCIETY or MECHANICAL ENGINEERS, 1941.

16 « The Flow of Water in Concrete Pipe, » by F. C. Scobey, Bulletin 852, U. S. Department of Agriculture, October, 1920.

6 Assistant in Mechanical Engineering, Princeton University, Princeton, N. J.

Discussion

R. L. DAUGHERTY.? The writer has nothing but commendation for this excellent paper. The author has presented the latest theory combined with the available experimental data in a manner which makes it more convenient for use than has been the case heretofore. His evaluation of relative roughness for different types and sizes of pipes is a step forward.

While this paper deals primarily with pipe friction it is interesting to note the suggestions made concerning the treatment of the flow in open channels. The latter has not been given the attention from the standpoint of rational analysis that has been devoted in the past to pipes. It is to be hoped that developments in this field may be made along the lines suggested by the author.

The author calls attention to the well-known fact that in the transition zone the Nikuradse curves for his artificial sand-grain roughness are quite different from those obtained with commercial pipes. The writer would like to know if the author has any explanation to offer for this marked difference.

C. W. HUBBARD.B This paper is of interest to engineers who must estimate fluid-friction loss closely for certain types of problems. Ordinarily the Manning type of formula is preferred, since the roughness value may be determined from the Lype of surface of the wall as contrasted to the Darcy formula where the roughness coefficient varies with the size of pipe and is difficult to estimate. The author’s Fig. 2 allows a quantitative wall roughness estimated from the type of wall to be used.

During some recent tests made to select a protective paint for steel which would also have a low friction loss, it was found that several coatings, particularly those consisting of certain bitumastic constituents which required them to be applied thickly to the wall, gave low flow-resistance values. The tests, made in 3-in. pipes, which were split longitudinally to allow proper application of the coating, showed roughness values of the order of those obtained with drawn-brass tubing. However, the appearance of the coating was not as smooth as drawn tubing. The writer had previously experienced this effect with similar coatings. There seems to be little published material on the friction loss produced by various protective paints and coatings on pipe walls, particularly on small pipes when the flow is likely to occur in the transition range where the friction loss is dependent upon Reynolds number. Apparently the roughness of such surfaces is of the wavy Gype which cannot be evaluated on the same basis as the same magnitude of roughness which is of the granular type.

A. T. IPPEN.9 The author has ably satisfied the object of his paper stated in the beginning with an extremely timely and practical summary of the latest information available on pipe friction. Academic research in this field over the last 30 years conducted on a fundamental basis has finally yielded a satisfactory explanation of the nature of the laws of pipe friction and has cleared up the concepts of energy dissipation in conduits and channels.

? Professor of Mechanical. Engineering, California Institute of -Technology, Pasadena, Calif.

Lieutenant Commander, U.S.N.R. Mena. A.S.M.E.

Assistant Professor, Hydraulic Laboratory, Lehigh University, Bethlehem, Pa.

The evidence for the adoption of the methods for, determining the pipe friction factor as presented by Colebrook is rather astonishing. Some experiences in this connection may be contributed here. The writer has computed two comprehensive sets of data on, pipe friction, one by John R. Freeman and another by L. H. Kessler. The former completed his experiments during the years 1889 to 1893 and his data were published by this Society in a special volume (15)10 in 1941. The second set of data was obtained from pipe friction experiments at the Wisconsin Experimental Station, the results of which were published in 1935. Both experimenters performed tests on 1/4 in- to 8 in diameter wrought-iron pipes in new condition covering the maximum range in Reynolds numbers possible under their experimental conditions. After plotting these results every one of their rails shows essentially the f versus R curve indicated by Colebrook and ‘e values calculated for all the various sizes come out very close to the average value stated for wrought-iron pipe in the present paper. It must be remembered that Kessler’s data were obtained 40 years after those of Freeman and that it can hardly be assumed that manufacturing processes remained identical during that period.

Another fact of importance to the practical engineer from this analysis of Freeman’s and Kessler’s data is worth mentioning. Rouse and Moody in their f versus R curves terminate the transition range from smooth- to rough-pipe flow along a line corresponding to a ratio of absolute roughness e to the laminar boundary layer thickness a of 6.08. Kessler’s and Freeman’s data do not give a single value that high in all their runs; their highest values obtained were about = 2.5. Under practical conditions of use therefore the flow of water in pipes occurs well in the transition range from smooth-to rough-pipe flow.

This fact easily explains why a final solution of the pipe friction problem was possible only after the concepts of « smooth-pipe » and « rough-pipe » flow had been established separately. While Nikuradse’s results on uniformly sand-coated pipe were helpful in this respect, they also resulted in more complicated transition curves than are obtained from tests with the statistical roughness patterns encountered of the most commercial pipe surfaces. The Colebrook universal function seems to fit the better in this transition range; the more, the roughness irregularities are statistically distributed as fax as size and shape are Concerned and vice-versa, the more regular the size and pattern of the irregularities the closer Nikuradse’s transition curves are approached, where finally the critical velocity for all roughness bodies is the same in the ideal case of completely uniform size.

The familiar functions for the pipe friction factor f may be written in the following form

1, Numbers in parentheses throughout the discussion refer to the Bibliography at the end of the author’s paper.

According to Colebrook, Equations, [1] and [2] are combined into the following universal function

This function reverts to either Equation [1] or Equation [2], if either the influence of the relative roughness disappears or when the viscous influence becomes insignificant. By use of Equation [3], the Colebrook function may be written in the alternative form

This equation clearly brings out the dependence of the pipe friction phenomena upon the thickness of the laminar boundary layer, i.e., on the viscosity of the fluid. It will be found in practical calculations that this influence is very seldom absent. The proposed ultimate value of

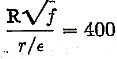
is equivalent to a value of

of 6.08.

It is evident that aging of pipes under varying conditions of use will result in new values of absolute roughness which at present are not easily’ predicted. From experiments on galvanized steel pipe of 4 in. diam at the Hydraulic Laboratory of Lehigh University, an initial average value of e = 0.00045 ft was obtained. This value of e was doubled within 3 years as a result of the change in surface conditions with aging under moderate conditions of use. It must be remembered here that this change in e represents only about a 20 per cent increase in the Darcy-Weisbach factor f, since the e value is a much more sensitive indicator of pipe roughness than the factor f.

In conclusion, it may be hoped that this paper will bring the general adoption of this relatively easy and reliable method of determining pipe friction and thereby establish a standard procedure in practice which is based upon sound analytical and experimental evidence.

W. S. PARDoE.11 In the following tests on pipes of various diameters and materials, the exponent n in the exponential formula,

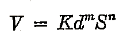
varied from 0.535 to 0.546, thus checking Williams’ and Hazen’s formula

very closely.

The maximum value of R was about 1,250,000 for 8-in. Neoprene dock-loading hose (very smooth) which is much below the « complete turbulence zone. » The tests included:

6-in. halite cement-asbestos pipe (predecessor of Transite)

4-in. Ruberoid cement-asbestos extruded pipe

4-in. fiber conduit

6-in, and 8-in. Neoprene dock-loading hose for E. I. du Pont de Nemours

2-in. to 12-in. steel pipe

8-in. rubber dock-loading hose with 1-in. X 1/8-in. helical metal band on inside

In no case except the last did the exponent n show even a tendency of decreasing, let alone approaching a value of 0.5 or complete turbulence. This must be due to the smoothness of the materials and the low value of Reynolds number. In the last case, the values of f did show a tendency to become constant, the value of e/D being quite large.

11 Department of Civil Engineering, University of Pennsylvania, Philadelphia. Pa,

The writer has not conducted a sufficient number of tests on pipes and is far from a pundit on this subject. At some time in the future, he will attempt to -work into the « complete turbulence zone, » if such there is, even if he must use a bit of 4-in. turberculated cast-iron pipe.

Mr. Pigott in his discussion has mentioned my insistence on the fact that the coefficients of Venturi meters become constant. This coefficient may be approximated by the formula

in which if β is the diameter ratio d₂/d_l and K is the coefficient of loss in

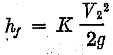
The value of K on the flat part of tests of 85 cast-iron Venturi meters approximates

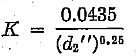
As the absolute roughness is constant, the proportional roughness varies inversely as the diameter or the coefficient increases with the diameter. The tests ran to quite high values of Reynolds number in terms of

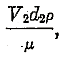
thus indicating there is such a thing as complete turbulence. Solving the foregoing expression

Hence a constant value of c gives a constant K, or n_f varies as V².

This is of course arguing from the writer’s experience with Venturi meters to make up for his lack of adequate experimental knowledge of the subject under discussion.

Professor Moody says f is a function of « two and only two », dimensionless quantities     

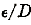
      and 

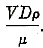
The writer has found in his work on Venturi meters a variation of over 1/2 per cent, due to the effect of the ambient temperature.12

As a variation of 1/2 per cent in c requires a variation of 25 per cent in k it seems to the writer the effect of a difference of temperature of 20 deg F on f at low value of R might be considerable. This effect is brought about by a change in the boundary shear; thus

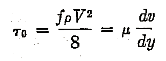
If Q is kept constant dv/dy will also be constant, and        corresponds to the temperature of the inside wall of the pipe, which will lie between the ambient temperature and that of the water. It will decrease as the velocity increases as a result of the heat being conducted away more rapidly. This the writer will check in future experiments; it may throw some light on the upper limit of the critical or unstable zone. The effect is a function of Reynolds and Prandt’s or Nusselt’s numbers, and the writer is not certain « what the price of cheese in Denmark does to effect f”.

12 « Effect of High Temperatures and Pressures on Cast-Steel Venturi Tubes, » by W. S. Pardoe, Trans. A.S.M.E., vol. 61, 1939, p. 247.

Professor Moody is to be congratulated on producing a very usable plot of friction factors which in due time may replace the Pigott and Semler curves which have to date been extensively quoted and used by engineers. Thus do we progress?

R. J. S. PioarT.13 This study of friction factor in pipes is particularly interesting to the writer, as it is a valuable further rationalization of a situation which has been unsatisfactorily empirical.

At the time the writer’s own correlation (4) was presented (1933) there was almost complete lack of uniformity between various formulations in general use, wandering all the way from Sutter, Hazen, and Williams tables, to Aisenstein’s averaged values.

There was great need to prepare a formulation that would work satisfactorily for all kinds of conduit, from brass tubing to brick ducts, and for all fluids.

Dr. Kemler, then on the writer’s staff, did the laborious part of the job, in correlating the results of all the experiments published up to that time, culling all those with incomplete data (6). The writer summarized this work, in form for direct application generally, introducing the roughness effect by rather strong-arm empiric; but at any rate the resulting chart worked well and has been growing in use.

The great value of the author’s study is that it puts the roughness effect, at last, on a much better justified basis. For example, Buckinghara (Fig. 1, reference 5) drew the lines for different sizes of steel pipe curved as they approached the viscous region, the same as the author now shows them; Stodola (Fig. 1, ref. 5) shows them straight and intercepting.

The later material used by the author shows that they are curved. Another important point settled by the author is that the lines for all roughnesses finally reach a constant value. The point at which this condition obtains is plainly shown to be a function of relative roughness, and so solves a difficulty Dr. Semler and the writer had, in correlating some of the test material. Some of the experimental results showed rather flat coefficients that were unexpected in regions of moderate roughness. But this constant value of f is confirmed by Professor Pardoe’s findings on Venturi discharge coefficients. He has been pointing out for years that the coefficient reaches a constant value at some Reynolds number that increases with size. Since most Venturis above rather small sizes are made with cast approach cones and the losses are substantially represented by pipe friction, this situation corresponds to flat final value of f at complete turbulence, and a decrease of the value of f with decrease of roughness.

Some engineers may be interested in the flow of queer materials like greases, muds, cement slurries, etc., that have thixotropic properties (quoted from the theologists), that is, they have plasticity mixed in with viscosity. All these materials have apparent viscosities ‘which decrease with increase of shear rate, but, when they finally reach turbulent flow, behave like true liquids of rather low viscosity. Such activities as oil-well drilling, cement-gun and grouting operations, automotive greasing equipment, and ball bearings involve such materials. In food industries, one gets tomato ketchup and pea soup; glue and soap solutions, paint and varnish operations, and various queer materials in the rayon and plastics industries. For those interested, a paper¹⁴ by the writer presents more or less a rational solution that has been quite satisfactorily supported by tests.

^{13 Chief Engineer, Gulf Research and Development Company, Pittsburgh 30, Pa. Fellow A.S.M.E.}

^{14 « Mud Flow in Drilling, » by R. J. S. Pigott, Drilling and Production. Practic A.P.I., 1941, pp. 91-103.}

In Fig. 1, the author has drawn his dotted line of complete turbulence somewhat in advance of the Reynolds number values at which the friction factor becomes a constant quantity. The writer finds that the expression

represents, as closely as can be determined from the small-scale diagram, the point at which the friction factor becomes absolutely constant. It is curious and probably only accidental’ that the value 3500 corresponds about to the upper limit of the critical zone.

RousE.15 Important results of laboratory research frequently do not reach the hands of practicing engineers until many years after the original papers have been published. A salient case in point is the discovery by Blasius in 1913 of the dependence of the Darcy-Weisbach resistance coefficient, f upon the Reynolds number R, which did not come into general engineering use until perhaps a decade ago. It often happens, however, that once engineers have accepted a new idea they are loath to modify it in any way. The paper under discussion is a very commendable endeavor to make recent experimental findings immediately useful to the engineer, but the writer feels that it still caters to a regrettable degree to the engineer’s innate conservatism.

If the writer’s belief is correct, this paper is intended to fulfill the same purpose as that which prompted the writer to present a somewhat similar paper (12) and resistance chart at the Second Hydraulics Conference in 1942. The author claims that’ in this chart, which is reproduced herewith in slightly modified form,¹⁶ the writer adopted co-ordinates inconvenient for ordinary engineering use. Such criticism resulted from the writer’s deliberate advancement beyond the now familiar Blasius f-versus-R notation in the belief that both greater convenience and greater significance would be attained thereby. Since these two papers of identical purpose thus differ in their basic method of approach, a criticism of the one point of view must necessarily involve a defense of the other.

Although Blasius’ original dimensional analysis of the variables involved led to his adoption of the form VD/ν as the most significant grouping of terms upon which f should depend, it must be realized that the following three different combinations of the same variables are all equally valid for the basic case of a smooth pipe: ¹⁷

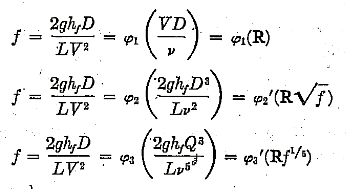
The combination now most familiar to the engineer, of course, is the first, although it has long since been proved that it will yield a linear plot on logarithmic paper for only the laminar zone. The second, on the other hand, is the basis of the Karman-Prandtl analysis of the turbulent zone, the general functional relationship simply being written in the specific form:

^{15 Director, Iowa Institute of Hydraulic Research, University of Iowa, Iowa City, Iowa.}

^{16 « Elementary Mechanics of Fluids, » by Hunter Rouse; John Wiley & Sons, Inc., New York,- N. Y. (in Press).}

^{17 « Solving Pipe Flow Problem with Dimensionless Numbers, » by A. A. Kalinski, Engineering News-Record, vol. 123, 1939, p. 23.}

Despite the author’s, indication to the contrary, f is not inextricably embodied in the second term of this relationship, as may be seen from the identity

If the Karman-Prandtl parameters are chosen as the basis of a semi logarithmic chart, as in the accompanying figure, not Only will the smooth-pipe relationship plot as a straight line, but all transition curves from the smooth to the rough relationship will be geometrically similar. It would appear to the writer that this combines ease in interpolation (and hence convenience) with greater significance than the Blasius plot will permit. This, therefore, is one of the writer’s two reasons for continuing to recommend the newer type of chart in preference to that of the author.

The writer’s second reason will be evident after further inspec­tion of the foregoing functional relationships. The first relation­ship will be directly useful in graph form only if the velocity or rate of flow is known; otherwise the desired coefficient may be evaluated from the graph only through the inconvenient process of trial and error. If the velocity or rate of flow is not known, on the other hand, a graph of the second functional relationship will make the desired coefficient immediately available. In order to provide a single chart which would satisfy both sets of requirements, the writer supplied ordinate scales of both f and  

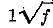
(the latter being proportional to the Chezy C) and abscissa scales of both R= V.D/ ν and

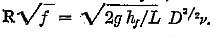
Since the parameters     

were selected by the writer for the primary ordinate and abscissa scales; the alternative abscissa parameter     

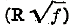
is necessarily represented by curved lines over a portion of the writer’s chart. Had log f and log R been chosen as the primary parameters,   

would still have required sloping lines in the grid; such choice therefore in­volves no particular advantage over the writer’s but rather de­feats the writer’s purpose owing to the accompanying distortion of the entire system of transition curves. The author’s graph, of course, contains no secondary grid system simply because it permits direct solution for only one of the several variables.

Brief mention might be made of the third possible combination of variables, which is evidently applicable to problems in which the diameter is the unknown quantity. So long as the pipe is smooth, such a plot will be of use, but the adoption of a similar function for the case of rough surfaces will still require a trial-and­-error solution, unless the graph is made hopelessly complex, ow­ing to the fact that for a given boundary material the pipe di­ameter must be known, before the relative roughness may be evaluated. Solution by trial might therefore proceed just as well from either of the other two functional relationships con­tained in the writer’s diagram.

The writer commends the author’s presentation in graph form of the values of absolute roughness given in the writer’s paper, but notes with interest that this plot is consistent with the writer’s rather than the author’s choice of basic parameters. Such a graph would therefore have its greatest value when prepared as a marginal extension of the writer’s resistance chart, for then no relative-roughness computations would have to be made.

So far as the author’s discussion of open-channel resistance is concerned, the writer takes exception to two points of fundamen­tal importance: First, the author states that such relationships as the Manning formula should be used in open-channel computa­tions in preference to values derived from pipe tests, implying that the familiar empirical open-channel formulas are inherently more valid. It is known, however, that the Manning formula (not to mention those of Bazin and gutter) is not in accordance with the logarithmic law of relative roughness upon which the author’s paper is based. So far as the writer can ascertain, the only reason pipe tests could not generally be used in evaluating open-channel resistance lies in the fact that few open-channel boundary surfaces are suitable to testing in pipe form. Aside from the moot question of the effect of cross-sectional shape (which the empirical open-channel formulas in no way answer), it would appear to the writer that a general resistance graph for uniform open channels should differ little from that for pipes, ex­cept in that the familiar parameters C and S might conveniently be included in the co-ordinate scales; this has been done in the present form of the writer’s chart.

The writer’s second objection to the author’s closing section is in regard to his implication that the Froude number should re­place the Reynolds number as the fundamental resistance pa­rameter for open-channel flow. So far as boundary resistance is concerned, the writer can see no possibility of the Froude number playing a comparable role. It is true that viscous shear is of little significance in comparison with boundary roughness in most open-channel problems, but it is also true that the effect of sur­face waves upon the internal resistance to flow has not yet been ascertained. The open-channel problem is, in fact, quite analo­gous to that of ship resistance, in which the matter of surface drag is considered wholly independent of the Froude number. If, to be sure, the phenomena of slug flow, atmospheric drag, and air entrainment prove to govern the resistance in the comparatively infrequent case of supercritical flow in open channels, then the Froude number may well become an appropriate resistance criterion, as it already is for cases of channel transition. But to imply that it should replace the Reynolds number as a resistance parameter whenever a free surface exists seems rather untimely to the writer, in that it could lead to serious misinterpretation of those few principles of boundary resistance which have been definitely established.

^{1, Professor of Engineering Research, The Pennsylvania State}

^{College, School of Engineering, State College, Pa. Mena. A.S.M.E.}

^{19 « Mechanism of Disintegration of Liquid Jets, » by P. H. Schweitzer, Journal of Applied Physics, vol. 8, 1937, pp. 513-521.}

P. H. Schweitzer.¹⁸  Lest the author’s charts, presented in delightfully handy forms, be used indiscriminately, it is perhaps in order to add one note of caution. Most of the statements, formulas, and charts are valid only for « long » pipes. For short pipes, the rules controlling turbulence are different, and Reyn­olds number is not the sole or deciding criterion for the state of flow.

If the velocity of flow in a long tube is decreased below the « critical » value, a change from turbulent to laminar flow takes place rather abruptly. The author sets the indeterminate region between 2000 and 4000 Reynolds number. Even that represents a rather narrow strip in the total range covered by the flow of such liquids as water or light oil. Outside of this indeterminate region, the flow is either completely laminar or decidedly turbu­lent, ignoring the rather thin laminar-boundary layer.

While this is true of relatively long tubes, for short tubes or nozzles it is not. In a short tube, as was shown by the writer, ¹⁹ the normal state may be, described as « semiturbulent flow, » which may be visualized as a turbulent core in the center and a laminar envelope near the periphery. The thickness of the laminar envelope may vary between wide limits. The change from turbulent to laminar flow or the reverse takes place in a short tube so gradually that the intermediate stage usually covers the whole practical region.

Of course, in both long and short tubes, turbulent flow is pro­moted by high flow velocity, large tube size, curvature of the tube, divergence of the tube, rapid changes in direction and cross-sectional area of the tube. Laminar flow is promoted by high liquid viscosity, laminar approach, rounded entrance to the tube, slight convergence of the tube, absence of curvature and disturb­ances.

Irrespective of the length of the tube an originally turbulent flow will remain turbulent, if its Reynolds number R = vd/ν is greater than the critical Reynolds number; conversely, an originally laminar flow will remain laminar if R is lower than the number.

If the flow at the entrance is turbulent but its Reynolds num­ber in the tube is lower than the critical, the flow will turn purely laminar if the tube is straight, reasonably smooth, and sufficiently long. If the flow at the entry of the tube is laminar but its Reyn­olds number is above the critical, it is hard to predict the charac­ter of the ensuing flow. If the entry is smooth and rounded and the tube free from disturbances and irregularities, the flow will remain laminar even at Reynolds numbers » as high as 15,000.

In a complete absence of all disturbances, a laminar flow proba­bly never turns turbulent, no matter how high its Reynolds number, but the slightest disturbance will ultimately cause tur­bulence if the Reynolds number is above the critical. The higher the Reynolds number the greater the disturbance, the shorter the tube travel necessary for turbulence to set in.

In a short tube the critical Reynolds number is not the one above which the flow generally or in a particular case is turbulent. The flow is frequently laminar at Reynolds numbers above the critical and it may be turbulent or semiturbulent at Reynolds number below the critical.

The critical Reynolds number is the one below which, in a straight long cylindrical tube, disturbances in _.the flow will damp out. Above the critical Reynolds number disturbances (ap­proach, entry, etc.) never damp out, no matter how long the tube is. The critical Reynolds number so defined was found by Schiller²¹ to be approximately 2320.

In short tubes, or nozzles, the length is not nearly enough for the flow to assume a stable condition. Under the circumstances, a Reynolds number higher than critical will have a tendency to­ward turbulence and vice versa, but it may take a tube travel of 60 times diameter before a stable velocity distribution is de­veloped. The actual flow in the nozzle will be influenced con­siderably by the state of flow before the orifice and the disturb­ances in the approach and within the nozzle. The combination of these factors in addition to the Reynolds number will deter­mine the state of turbulence at the exit of the short tube. For a given short tube or nozzle, the influence of the nozzle factors can be considered the same; therefore the Reynolds number alone will determine the character of the flow.

With decreasing Reynolds number, the thickness of the laminar layer increases and the turbulent inner portion decreases until it finally disappears. It is peculiar to nozzles or short tubes that the change from turbulent to laminar flow (or vice versa) takes place gradually rather than abruptly. The semiturbulent state extends over a wide range of Reynolds numbers, differing only in the relative thickness of the turbulent core and laminar envelope.

^{20 With a convergent tube of 10-deg cone angle Gibson (Proceed­ings of the Royal Society of London; vol. A83, 1910, p.. 37G), observed; laminar flow at R = 97,000.}

^{21 « Untersuehungen, fiber laminare and turbulente Stremung, » by L. Schiller,            Forschungsarbeiten, vol. 248}

AUTHOR’S CLOSURE

The paper was intended for application to normal conditions of engineering practice and specifies a number of qualifications limiting the scope of the chsrts, such as their restriction to round (straight) new and clean pipes, running full, and with steady flow. Under such conditions it was stated, as noted by Professor Par-doe, that the friction factor f « is a dimensionless quantity, and at ordinary velocities is a function of two, and only two, other dimensionless quantifies, the relative roughness of the surface and the Reynolds number »

Under abnormal conditions f could of course be affected by other dimensionless criteria. In closed conduits at very high velocities or with rapidly varying pressures it depends on the Mach or Cauchy number introducing the acoustic velocity. In open channels, as pointed out, free surface phenomena, gravity ‘waves, make it logically dependent on Froude’s number. At very low velocities in shallow open troughs it would conceivably be controlled also by the Weber number for surface tension and capillary waves. Capillary forces while important to insects, as to a fly on flypaper, are negligible to us in problems of engineering magnitude. Under usual conditions of pipe flow only the two dimensionless ratios mentioned need be considered, and it is possi­ble to present the relations between the factors in a chart such as Fig.1.

The discussions have brought out a number of other departures from normal conditions and further limitations to the scope of the charts. Professor Pardoe reminds us that a considerable temperature difference between the fluid and pipe wall may have a measurable effect on the shear stresses, due to ambient currents which would increase the momentum transfer in similar manner to turbulent mixing. This effect would probably be of impor­tance only at .the lower Reynolds numbers and with material temperature differences.

Mr. Pigott reminds us that the scope is limited to simple fluids and does not cover « queer materials like greases, muds, cement slurries » and mixtures with suspended solids. Professor (now Commander) Hubbard and Professor Pardoe mention some un­usual forms of pipe surfaces. The author thinks that most of these, including paint coatings, will follow the lines of the charts closely enough for practical purposes if the proper roughness figures are determined; but the rubber dock-loading hose with helical internal band will probably follow a curve similar to curve V in Fig. 6, which Colebrook and White obtained for spiral-riveted pipe.

Dr. Ippen mentions the rate of increase of roughness from corrosion and gives some useful test information. Colebrook found that corrosion usually increases the value of E at substan­tially a uniform rate with respect to time. Professor Schweitzer calls attention to the point that the pipe must be long, with an established regime of flow, and that the charts do not apply to the entrance or « smoothing section » which require separate allowances. Fortunately we are seldom concerned with close estimates of friction loss in short tubes, where friction is a minor element in the total loss of head.

Dr. Ippen’s discussion admirably summarizes the basic struc­ture of the charts and gives supporting evidence. His own studies of the problem had, the author believes, led him inde­pendently to conclusions similar to Colebrook’s.

The Colebrook function has given us a practically satisfactory formulation bridging the previous gap in our theoretic structure, a region in which the majority of engineering problems fall. It has the further useful property of covering in a single formula the whole field of pipe flow above the laminar and critical zones;- and throughout the field agrees with observations as closely as can be reasonably demanded within the range of accuracy available in the measurements, particularly in the evaluation of the boundary roughness.

Referring to a question raised by Professor Daugherty, the in­consistency between Nikuradse’s tests in the transition zone and those from commercial pipe is usually attributed either to the close spacing of the artificially applied sand grains, such that one particle may lie in the wake behind another, or to the uniformity of Nikuradse’s particles in contrast-to the usual commercial sur­face, which is probably a mixture of large and small roughnesses distributed at random. The latter explanation seems particu­larly plausible, since a few large protuberances mixed with smaller ones could project far enough into the lsminnx boundary layer to break it up, while a uniform layer of projections of av­erage size would all remain well within the same thickness of layer. Thus Nikuradse’s curve clings closely to the smooth pipe line much farther thanthe curve for commercial surfaces. At any rate the artificial character of Nikuradse’s surfaces weighs against the use of his values in the region where the discrepancies appear.

Mr. Pigott reviews the progress in charting friction factors and gives evidence supporting the laws adopted. At the end of his discussion he brings up an interesting question, the form and location of the dashed line in Fig. 1 marking the boundary of the rough pipe zone for complete turbulence, beyond which the fric­tion factors become practically horizontal. With his gift for detecting relationships he arrives at a modified equation for this curve.

Referring to Figs. 5 and 6 it will be noted that Nikuradse’s experiments on artificial roughness gave a curve. which dropped below the « rough pipe » line and then approached it from below, while ordinary commercial pipes give points which approach the rough pipe line from above, and that both sets of points seem to merge with the rough pipe line at about

which Rouse accordingly adopted as the equation of the boundary of the rough pipe zone, the dashed line shown in. Fig. 1. If, how­ever, we adopt the Colebrook function for the transition region to the left of this boundary curve, strictly speaking the Colebrook curves never completely merge with the constant f lines but are asymptotic to them; so that on the basis of the Colebrook func­tion there is no definite boundary to the rough pipe region.

Practically however the Colebrook function converges so rapidly to the horizontal lines that beyond Rouse’s dashed curve the differences are insignificant. Considering the practical difficulties of measurement and consequent scatter of the test points, and the fact that the Colebrook function is partly empiri­cal and merely a satisfactory approximation, it seems hardly justifiable to draw fine distinctions from an extrapolation of this function. If the function could be accepted as completely rational it would be more logical to locate the boundary curve so that it would correspond to some fixed percentage of excess in f over the f for complete turbulence.

Prompted by Mr. Pigott’s suggestion, the author has analyzed the Colebrook equation from this point of view. Calling f the value of the friction factor according to Colebrook, and f_k the value for complete turbulence according to von Karman, the Colebrook equation can be expressed

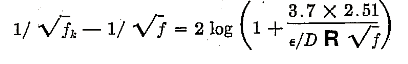
Calling

a small quantity compared to 1 (of the order of 0.05 or less in the region of the boundary curve) then log (1 + x) can be expanded in a series giving

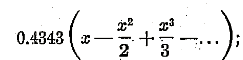
and neglecting x² and higher powers

If now we denote by s the proportional change in f, that is

 being small compared to 1, then

which, expanding by the binomial formula„ is very nearly

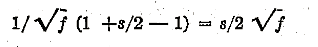
Hence:

is the proportional change in f caused by the Colebrook function.

In plotting Fig. 1, the author, instead of continuing indefinitely with the insignificant effect of the small term, and favoring the view that f should became substantially constant in the rough pipe zone, adopted the compromise of ignoring the variation when it fell below about one half of one per cent; and beyond this point the lines were drawn horizontally at the Ktirman value. That is the chart applied the Colebrook formula only to the transition zone.

Putting  

, we have      

practically confirming Mr. Pigott’s deduction. If we adopt a one per cent varia­tion off as a reasonable allowance, the boundary curve could be plotted from    

It might be more logical, to be con­sistent with the Colebrook function, to use this formula for the boundary curve instead of Rouse’s form. The two curves differ but little, and the choice seems more a matter of academic prefer­ence than practical importance; the scatter of test observations obscures a final answer.

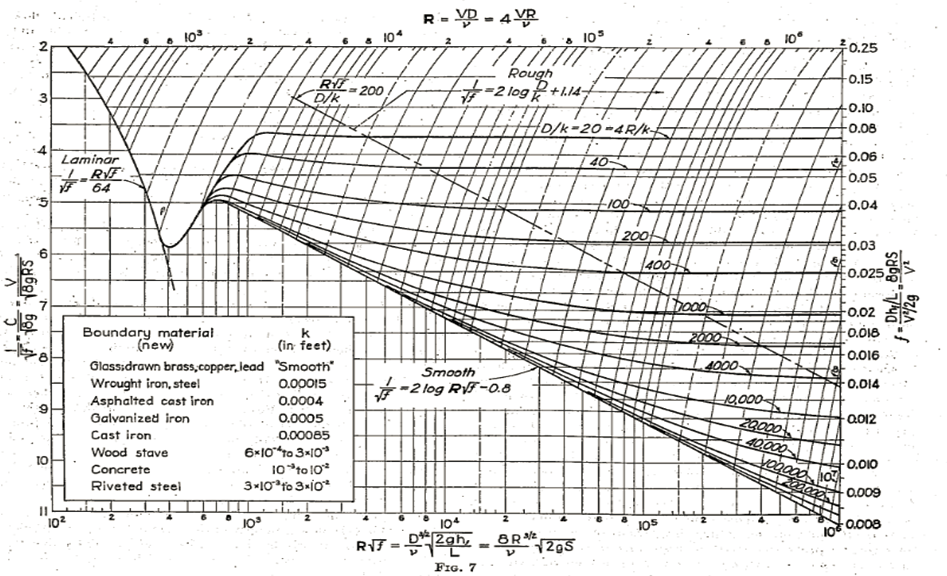
As noted in numerous references in the paper the author has been indebted to Professor Rouse for his contributions to the subject, particularly his valuable paper at the Iowa Hydraulic Con­ference. Professor Rousse’s inclusion in his discussion of his chart, Fig. 7, from the latter paper, is a useful addition to the material here collected. The co-ordinates selected for this chart bring out the functional relationships in a simple manner; and those who prefer to adopt this form of chart now have it at hand.

The author still considers it less convenient for usual engineer­ing problems than his Fig. 1. While the horizontal scale of Fig. 7 can be expressed in terms of the frictional loss of head in place of f, this is of no help where the velocity is given and the friction loss is to be found, nor is it of much help in usual engineering problems where the total head is given and the velocity is to be found. The total head almost always includes not only the friction loss in a pipe system; but also the exit loss, and the losses at entrance and in fittings, bends, and changes in section; and we can seldom assign in advance the value of the friction head or slope of the hydraulic gradient; so that successive approximations or trial- ­and-error solutions are still required. While Rouse’s chart is easier to construct, for the reasons explained the author adopted the form of Fig. 1 as easier to use.

Regarding the author’s suggestions as to open channels, the questions raised by Professor Rouse are probably due mainly to the omission of fuller explanation in the paper. It was not the intention to imply that at low velocities in relatively smooth open channels the friction loss would be independent of Reynolds Xi^–umber, and it may well be found that in- this region the loga­rithmic laws may continue to apply, at least in modified form, and that, as Professor Rouse states, « a general resistance graph for uniform open channels should differ little from that for pipes. »

The author was speaking of another region, « open channels dealt with in engineering practice…usually rough-surfaced and of large cross section, corresponding to large Reynolds numbers and falling in the zone of complete turbulence. » With fairly high velocities, corresponding to large Reynolds numbers, in the presence of a free surface, dimensional considerations require us to include the Froude number as a criterion; and in the region of complete turbulence we can fortunately afford to omit the Reyn­olds number as a controlling factor so that we do not have too many variables to handle. The author did not intend to imply that the Froude number « should replace the Reynolds number as a resistance factor whenever a free surface exists » but only in the region described, which however is within the range of ordinary practice.

Professor Rouse recognizes that free-surface phenomena com­prise a factor in the problem; his objection to including the Froude number is merely that « the effect of surface waves upon the internal resistance to flow has not yet been ascertained— » which calls on us to investigate the effect rather than to ignore it. Certainly wave-making resistance is a very real factor both in ship resistance, and in open channel flow in the region of the gravitational critical velocity, Even in tranquil flow it still may have a measurable effect; the location of the maximum velocity point below rather than at the surface suggests an in­fluence of this factor.

The author is confident that Professor Rouse will agree with his belief that further research on open channel friction is much needed; and he commends such a project particularly to the civil engineers. Neither the f versus R charts nor such formulas as Manning’s, Sutter’s or Basin’s are believed to take into ac­count all of the major controlling factors, and a. statistical analy­sis of available data along the lines suggested, supplemented by further experiments, may yield working charts or formulas of great value to engineers.

It is regretted that Professor (now Major) Colebrook, who has-been serving in, the British Army since 1939, was unable to sub­mit a discussion. The author wishes to thank all of the discussers for their useful contributions, and also to thank Mr. Richard B. Willi for his able presentation of the paper at the Pittsburgh meeting on behalf of the author.

Explicit Approximations to the Solution of Colebrook’s Friction Factor Equation

D. J. ZIGRANG

and

N. D. SYLVESTER

College of Engineering and Physical

Sciences The University of Tulsa Tulsa, OK 74104

The friction factor equation developed by Colebrook (1939) for tubulent

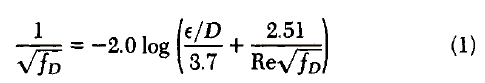
flow has received wide acceptance, probably because it was used by Moody (1944) in the preparation of his friction factor charts. However, Colebrook’s equation is implicit in Darcy’s friction factor, fv, and must therefore be solved by iteration, a formidable task in 1944 when Moody presented his charts which, no doubt, ac­ counts for their popularity. Solution of Eq. l by numerical methods to any desired degree of precision is accomplished easily, quickly and cheaply with today’s digital computers.

Moody (1947) presented an explicit friction equation applicable to the

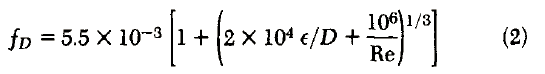
turbulent region of the flow. Equation 2 was said to yield friction factors within ±5% of those of Eq. l over the range 4,000       Re 107 and the relatively narrow range O                             f/D    0.01. Later we show that a maximum absolute deviation of 15.9% occurs for this equation if the maximum value for f/D is extended to 0.05.

A relationship developed by Wood (1966) for computer appli­ cation gives the Darcy friction factor explicitly as

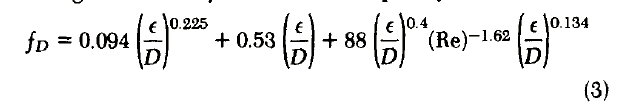
Our work shows that Wood’s equation has a maximum absolute

deviation of 6.0% over the ranges 4,000 <Re< 107 and 0.00004

< f/D <0.05. Jain (1976) used the theoretical equation of Von Karmen and Prandtl for rough pipes

with curve fitting to yield

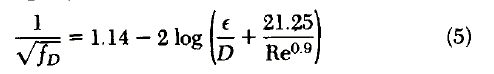
Equation 5 is said to differ from Eq. .l no more than 1% over the ranges 5,000 < Re < 107 and 0.00004 < E/D < 5 X 10- 2.

Churchill (1977) developed an explicit equation said to be ap­ plicable to all values of Reynold’s number and f/D,

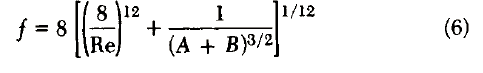
where

and

Chen (1979) presented an explicit equation which is superior to those of Moody, Wood, Jain and Churchill when compared to an iterative solution of Colebrook’s equation.

Equation 9 is also said to be good for all values of Re and f/D.

However it is compared with the equations of Colebrook, Wood

and Churchill only over the ranges 4,000 <Re< 4 X 108 and 5 X

10- 7 < E/D < 0.05.

Our purpose in this paper is to present two additional explicit approximations to the solution of Colebrook’s implicit equation. One of these is easier to U$e but less precise than Eq. 9 relative to the iterative solution of Eq. l while the second equation is both more complex and more precise than Eq. 9.

The turbulent portion of Moody’s chart includes 4,000 Re 108 and 10- 5 f/D   0.05 with a resulting range for Darcy’s friction factor of 0.001   fo  0.077. Using an average value of 0.04 for fo gives a value for the term 2.5226/    fo of about 13.

Combining this value with Eq. l gives

Combining Eqs. l and 10 yields

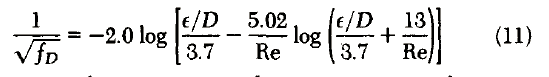
Equations l0 and 11 constitute explicit approximations for Eq. 1. Equation 11 is actually the first iteration in the numerical solution of Eq. l. The constant 13 in Eq. 10, which was selected on the basis

of an average value for fo of 0.04, proves to be very nearly opti­

mum over the range of interest and is much better value than is required by an iterative solution. Finally, Eq. 11 can be combined

with Eq. 1 to give

Equation 12 constitutes the second iteration in the numerical so­ lution of Eq. 1. It’s maximum deviation from the numerical solution of Eq. l is only 0.11%.

A numerical comparison of Eqs. 2, 3, 5, 6, 9, 11, and 12 with the

numerical solution of Eq. 1 was conducted. A matrix of 60 test points was formed combining each of 10 roughness ratioswith six different  values for Reynold’s number. The roughness ratios were 4 X 10- 5 , 5 X 10- 5, 2 X 10- 4, 6 X 10- 4, 1.5 X 10- 3, 4 X 10- 3, 8 X

10- 3, 1.5 X 10- 2, 3 X 10- 2 and 5 X 10- 2. The Reynold’s numbers

were 4 X 103, 3 X 104, 105, 106, 107 and 108. The absolute deviations relative to Colebrooks’ equation were computed from

and accumulated over the sixty points calculated for each of the seven explicit equations. The results are shown in Table 1.

Although each of the explicit approximations given in Eqs. 9, 11 and 12 is adequate for computational purposes, Eqs. 11 and 12 are recommended. Equation 9 requires more effort than Eq. 11 but less effort than Eq. 12. Likewise, Eq. 9·is more precise than Eq. 11 but less precise than Eq. 12. Consequently, Eq. 11 is recom­ mended for use with hand-held calculators because it is relatively simple for its degree of precision with respect to the Colebrook

equation equation. Clearly, Eq. 12 should be used with program­ mable calculators and digital computers.

NOTATION

D        = inside diameter of pipe E = Error, defined by Eq. 13 E = Roughness height

fv      = Darcy friction factor

fvc     = Darcy friction factor calculated from the Colebrook equation

Re       = Reynolds number

LITERATURE CITED

Chen, N. H., « An Explicit Equation for Friction Factor in Pipe, » Ind. Eng. Chem. Fund., 18(3), 296 (1979).

Churchill, S. W., « Friction-Factor Equation Spans All Fluid Flow Re­ gimes, » Chem. Eng., 91 (Nov. 7, 1977).

Colebrook, C. F., « Turbulent Flow in Pipes with Particular Reference to the Transition Region between Smooth and Rough Pipe Laws, »]. of Inst. Civil Eng., 133 (1939).

Jain, Akalank K., « Accurate explicit equation for Friction Factor, »]. Hy­

draulics Dtv. ASCE, 102 (HY5), 674 (1976).

Moody, L. F., « Friction Factors for Pipe Flow, » Trans. ASME, 66,641 (1944).

Moody, M. L., « An Approximate Formula for Pipe Friction Factors, »

Trans. ASME, 69, 1005 (1947).

Wood, D. J., « An Explicit Friction Factor Relationship, » Civil Eng., 60 (Dec., 1966).

Manuscript received October 17, 1980, reooion received April 3 and accepted April

23, 1981.

Friction-factor equation spans all fluid-flow regimes

A single correlating equation relates pipe friction loss to Reynolds number and surface roughness for laminar, transitional and turbulent flow alike, thus making fluid-flow calculation simpler.

StuartW.Churchill,UniversityefPennsylvania

Equations are more convenient than tables or graphical correlations in computer-aided design and operation. A single equation that correlates the fluid-flow friction factor with all Reynolds numbers and all pipe-roughness ratios can be constructed from theoretical and correlating equations for the laminar, transition and fully developed turbulent regimes of flow, using a general mode! developed by Churchill and Usagi [1].

The friction factor considered herein is defined in terms of the shear stress on the pipe wall, as follows:

The shear stress at the wall can be related to the gradients in pressure, elevation and velocity by a force and momentum balance, such as:

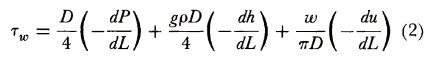
This equation is exact if the momentum-mean velocity is used in the right-hand derivative. However, the volumetric-mean velocity (3)

provides a reasonably accurate approximation.  We can then rewrite Eq. (2) more conveniently in terms of fluid density and mass flowrate by combining Eq.(1) and (2) and replacing u with w and p through Eq. (3), yielding:

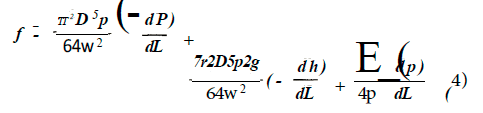
The friction factor defined by Eq. (l) and expanded in Eq. (4) is related to the commonly used friction factors of Fanning and Darcy, as follows:

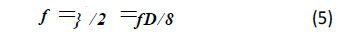
So, all equations in this article can be converted to the Fanning or Darcy friction factors, by multiplying the nonsubscripted fby 2 or 8, respectively.

The individual flow regimes

Laminar regime. For Re <2,100, Poiseuille’s law

f = 8/Re                                      (6)

is applicable.

Transition regime. The various sets of experimental data for the transition regime between laminar and turbulent flow are quite scattered. Wilson and Azad [2] obtained a precise set of values for the friction factor in smooth pipe -for 1,000 < Re < 500,000 by numerical computations. Using their values, we derive an empirical equation for the central portion of the transition regime:

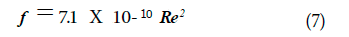
Experimental data suggest that this expression is reasonably valid for rough, commercial pipe as well. Turbulent regime in smooth pipe. Schlichting (3] and others have shown that the semitheoretical equation

of Prandtl expressed in the form of

gives a good fit for experimental data on smooth

G

pipe over the range 3,000 <Re< 3.4 X lQ . They

presume that Eq. (8) holds for even higher Re. For horizontal flow of a fluid of constant density,

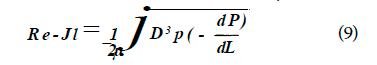
So Eq. (8) is convenient if the pressure gradient is specified.

However, Eq. (8) requires trial and error if instead the flowrate is specified. That difficulty is avoided by the Blasius equation:

However, Eq. (10) is inaccurate for Re > 10·5. The expression

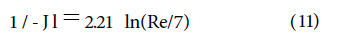
suggested by Colebrook (see Churchill [4]) is also convenient if the flowrate is specified, and is essentially

D     Diameter, m

Friction factor, Twf pu2

J;       Friction factor given by Eq. (i)

fn     Darcy friction factor, 8Twl pu2 fF           Fanning friction factor, 2Twf pu2

g Acceleration due to gravity, m/s2

h Elevation, m

L Length of pipe, m m Arbitrary exponent n  Arbitrary exponent P Pressure, Pa

Re Reynolds number, 4wj’ITµD

u      Velocity,

ub Volumetric-mean velocity, 4w/’7TD2p (m/s)

w    Mass flowrate, kg/s

!       Effective roughness, m µ        Viscosity, Pa· s

p     Density, kg/m3 Tw Shear stress, Pa

equivalent to Eq. (8) in accuracy. Eq. (8 ), (10) and (li) are applicable for !Re   fD    5 and Re    3,000, where ! is the effective (or surface) roughness; this parameter has been tabulated in Perry’s « Chemical Engineers’ Handbook » and elsewhere for v11rious kinds of pipe.

Fully developed turbulent .fiow in rough pipe. Nikuradse [5] determined the following asymptotic expression for very large Re in pipes having uniform artificial (laboratory-produced) roughness:

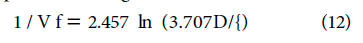
Eq. (12) also holds for rough, commercial pipe, and it is applicable for !Re        D         70 and Re           10,000. Developlng turbulent .fiow in rough and smooth pipe. Churchill [4] derived an expression for both developing and fully developed turbulent flow in both rough and smooth pipes by combining Eq. (8) and (12), as follows:

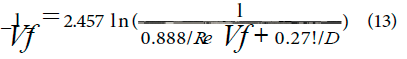
Eq. (11) was also combined with Eq. (12) to give an alternative expression:

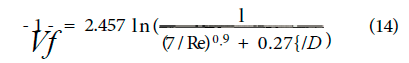
Eq. (14) differs only slightly from Eq. (13).

Eq. (13) is essentially equivalent to the expression commonly used to construct the complete turbulent regime of the friction-factor chart that is reproduced in most textbooks and handbooks.

The full-range equation

The friction factors given by Eq. (7) and (14) can first be combined in the form of the Churchill-Usagi mode! to yield the following test expression for the transition and turbulent regimes:

Here the subscripts 7 and 14 indicate Eq. (7) and (14), respectively. The computed values of Wilson and Azad   indicate   that   the best   value of the arbitrary constant n is about -8, hence:

Eq. (16) can m turn be combined with Eq. (6) in the form:

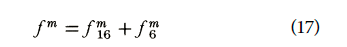
The computed values of Wilson and Azad suggest that, in this case, 12 is the best value for the arbitrary constant m, hence:

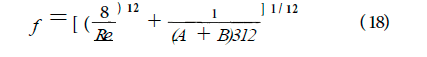
where

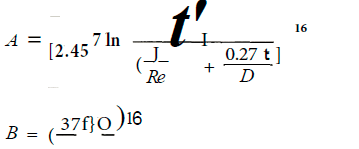
Eq. (18) is valid for ail Re and t:/ D. A trial-and-error solution is necessary if the pressure drop rather than the flowrate is specified, but this situation would also occur if Eq. (13) were used rather than Eq. (14).

Conclusions

Eq. (18) is a convenient and accurate replacement for ail of the friction-factor plots in the literature. The only uncertainty arises from the degree of accuracy ofcomponent Eq. (6), (7), (11) and (17), and from the experimental and theoretical values upon which they are based. The equation appears to be complicated but is actually suitable for calculations with even a hand-held computer.

This equation not only reproduces the friction-factor plot but also avoids interpolation and provides unique values in the transition region. These values are, of course, subject to some uncertainty, because of the physical instability inherent in this region.

References

l. Churchill, S. W., and Usagi, R., A General Expression for the Correlation of Rates of Transfer and Other Phenomena, A/ChE j., Vol. 18, No. 6, 1972, pp. 1121-1128.

2.Wilson, N. W., and Azad, R. S., A Continuous Prediction Method for Fully Developed Laminar, ‘l’ransitional and Turbulent Flows in Pipes, J.Aplud Mech., Vol. 42. 1975, pp. 51-54.

5.Schlichting, H., « Boundary Layer Theory, » 4th ed., p. N.Y., 1960.

4.Churchill, S. W., Empirical Expressions for the Shear Stress in Turbulent Flow in Commercial Pipe, AlChE J., Vol. 19, No. 2, 1973, pp. 375-376.

5. Nîkuradse, J ., Strômungsgesetze in rauhen Rohren, Ver. deutsch. lng., Forschungshdt 361, 19:n. T

The author

Stuart W. Churchill is the Carl V.S. Patterson Professcir of Chemical Engineering at the University of Pennsylvania, Philadelphia, PA 19174.

He obtained bachelor’s and doctoral degrees at the University of Michigan, gaining five ycars of industrial experience along the way. He served as Professor and Chairman of the Dcpartment of Chemical and Metallurgical Engineering at Michigan before moving to Penn. A past president and a fellow of AIChE, and a member of the National Academy of Engineering, he has done research mainly in heat transfer and combustion.